I use a semi-automated method implemented by a program which I have written in Matlab. Rather than a failure-prone automatic method of separating chanter and drone harmonics, the program helps the user to do it by eye.
I start with a .wav file. For example, here is John D. Burgess playing a bit of Bonny Argyle. Let's say we want to measure the high A in the middle of this passage. This is a bit of a challenge because all the chanter harmonics will be very close to those of the drones.
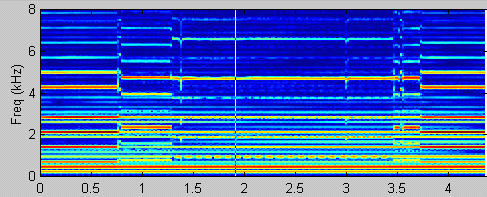
Step 1: Compute a spectrogram so we can see what's going on. The horizontal axis is time (in seconds) and the vertical axis is frequency (in kHz). Mark the time at which we want the analysis to be done (the light vertical bar at around 1.9 seconds).

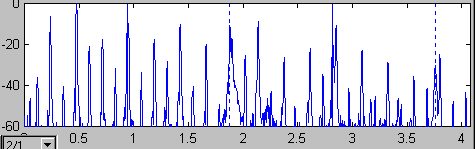
Step 2: Calculate an FFT on a short (200 ms) portion of the signal starting at this time
Step 3: Click on the lowest drone harmonic (in the vicinity of 100 Hz). The program then lays down a "harmonic grid" roughly marking all the drone harmonics ...
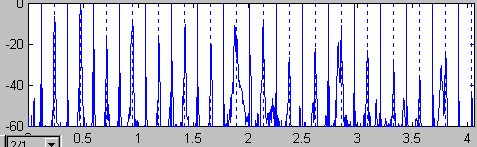
Step 4: For a very precise estimate of the drone fundamental, pick a good-looking, isolated upper drone harmonic, say the one just above 3.5 kHz. We can get a good estimate of its frequency by fitting a parabola to the peak in the spectrum and finding the vertex position. Because the harmonic grid is in place, the program knows that this is the 30th harmonic. We get the drone fundamental by dividing the selected peak's frequency by 30. This also improves the precision of the measurement by a factor of 30! The FFT itself has a resolution of 1/.2 or 5 Hz. The parabolic fit improves this by a factor of 10-20, and thus the "high harmonic" trick gives us the frequency within a fraction of a Hz. In this case the drone fundamental turns out to be 118.77 Hz (let's not take the last decimal place too seriously), suggesting that an octave high A should be at 950.16 Hz.
Step 5: Do steps 3 & 4 for the chanter harmonics. In the FFT we can see that each chanter harmonic lies slightly below the nearest drone harmonic. This agrees with what our ears tell us from the wave file; as usual, Mr Burgess's high A is well flat of an octave relationship with the drones. Here the high A turns out to be at 940.15 Hz, which is 18.3 cents flat to the drones.