
Journal
of Geographic Information and Decision Analysis, vol.1, no.1, pp. 9-24
Object-oriented
Simulation and Evaluation of River Basin Operations
René F. Reitsma
CADSWES/CEAE, University
of Colorado, Campus Box 421, Boulder, CO 80309-0421, USA
reitsma@cadswes.colorado.edu
http://cadswes.colorado.edu/~reitsma/
John C. Carron
CADSWES/CEAE, University
of Colorado, Campus Box 421, Boulder, CO 80309-0421, USA
carron@cadswes.colorado.edu
http://cadswes.colorado.edu/~carron/
ABSTRACT A
computational framework for the integration of physical process modeling
and multicriterion evaluation of river basin operations is presented. Despite
a rich tradition in water resources multiobjective programming, most real-world
water resources planning relies on simulation followed by ex-post multicriterion
evaluation. In this paper we present a computational framework for the
integration of modeling and ex-post evaluation by means of object-orientation.
Advantages are a simpler, less ambiguous software data model; concurrent
computation of physical and multicriterion aspects of a natural resource;
efficient locale-specific evaluations; and interactive, interest-specific
definitions of evaluatory views. The concepts are tested in the context
of simulating and evaluating Colorado River operations.
KEYWORDS:
environmental planning, multiobjective planning, multiobjective evaluation,
object-orientation, interest-specific evaluation, river basin management,
simulation, data model, decision support systems.
Acknowledgments This
research was sponsored by the Colorado Advanced Software Institute (CASI),
grant number 93-0003 and IBM Corporation, Boulder, Colorado.
Contents
1.
Introduction: The DSS Data Model for Environmental Planning
Environmental resource planning problems comprise a subset of the more
general class of public policy and resource allocation problems. As such,
they are complex in that they contain technical as well as organizational
and sociopolitical components which maintain complicated interrelationships
(Brenner 1973; Cohon 1978; Kaufman and Duncan 1990;
Glasbergen 1994; Purdy and Gray 1994). This complexity renders many
environmental management problems ill-structured or ill-defined. Bosman
(1983) defines ill-structured problems as those for which one of the following
conditions is not met:
-
The set of action alternatives is finite and identifiable;
-
Solutions are consistently derived from a model that shows good correspondence;
-
The effectiveness or efficiency of the action alternatives can be numerically
evaluated.
Since the second and third criterion
are necessary conditions for the application of multiobjective programming
(Cohon 1978; Rios 1994), other, less structured
approaches for the resolution of this class of problems have been developed.
One such an approach is that of decision support systems (DSS). Proponents
of these systems (Loucks et al. 1985; Fedra
et al. 1986, 1993; McLean and Sol 1986; Guariso and Werthner 1989;
Sprague and Watson 1993; Finlay 1994) propose that DSS offer multiple
representations of the decision problem, combined with facilities that
allow interactive assessment of the various aspects of the problem through
different models, data visualizations, multicriterion evaluations and reports.
The paradigm is simple, yet elegant. Rather than attempting to a priori
resolve and formalize the problem in its entirety, only easy-to-formalize
components are represented and augmented with software tools that allow
users to flexibly navigate the decision space. For environmental DSS, this
usually results in systems that are constructed around three main components
(Figure
1):
-
State information: representation of the environmental resource's
state at any point in time. For water resources this includes information
such as historical flows, reservoir storage and pool elevation, water and
energy demands, etc.
-
Process information: first principles governing the resource's behavior
over time. Simulation models representing a resource's dynamics or state
transition rules are part of this component;
-
Evaluation tools: models for transforming raw system data into information
relevant for decision making; e.g., multicriterion evaluation models, system
status checkers, report generators, etc.
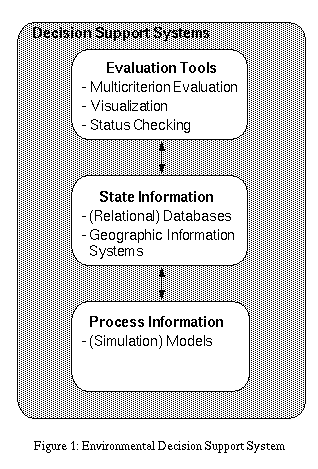
Figure
1 Environmntal Decision Support System
The remainder of this paper consists
of three sections. First, we explore some of the problems associated with
the above DSS architecture. Next, we introduce an alternative, object-oriented
architecture and argue that this architecture resolves some of these problems.
Finally, we illustrate the use of the approach by means of an application
of object-oriented multicriterion evaluation of streamflow regimes in the
Colorado River.
Although the conventional DSS architecture provides a viable basis for
the formulation of the functional components of an environmental DSS, it
is often problematic from a computational and implementational point-of-view
in that the different components have traditionally required different
software data models. For instance, state information is often represented
using relational and spatial (GIS) data models for attribute and spatial
data respectively, whereas process information is represented in simulation
models. Evaluation tools, in turn, are often implemented as specialized
software containing highly structured, formal techniques such as multicriterion
evaluation models (Nijkamp et al. 1990; Korhonen
et al. 1992), multiattribute preference models (Timmermans
1986; Timmermans and van der Heijden 1987), or more ad hoc techniques
such as data visualization or report generation. As a result, the traditional
architecture of environmental DSS is a collection of more or less independent
software components and data models, integrated through a complex infrastructure
of data pipes and channels, files and memory mappings (Reitsma
1990; Fedra 1991). The disadvantages of this kind of "dedicated" representation
are obvious: complex data logistics; highly specialized, nonmodular implementations;
poor technology transfer; and high maintenance and extension costs (Dames
and Moore 1993).
Associated with these logistic difficulties are other, more conceptual
problems. One of those concerns the problem of place- or locale-specific
plan evaluation. For instance, fish habitat studies of the Colorado River
have shown different empirical relationships between streamflow and habitat
suitability for different sections of the river, for the same fish species.
Likewise, a utility function for white water rafting based on streamflow
will have to vary by locale, because only through the interaction between
flow and channel morphology can a value for rafting utility be inferred.
For example, equal rates of flow in the lower Colorado and in one of its
headwater tributaries might result in optimal conditions in one locale,
and hazardous conditions in the other. The above DSS architecture, where
plan evaluation is implemented as a separate set of software applications,
makes it hard to conduct this type of analysis.
Formal ex-post plan evaluation methods such as multicriterion and multiattribute
preference models rely on algebraic utility functions or combination rules
such as additive (equation
1) or multiplicative exponential utility (equation
2) functions (Timmermans 1986; Timmermans and
van der Heijden 1987; Nijkamp et al. 1990; Korhonen et al.
1992).
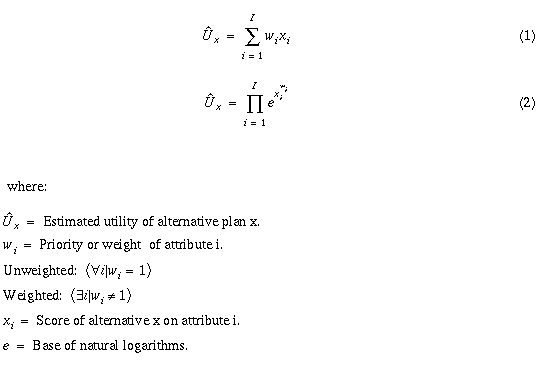
Recently,
a number of objections against this type of evaluation modeling have been
put forth (Hendriks and van der Smagt 1988; Reitsma
1990; van der Smagt and Lucardie 1991; Lucardie 1994). These objections
can be summarized by the assertion that algebraic utility functions rarely
adequately represent interest-specific evaluation of plans. As the various
authors point out, complex conditional relationships between evaluation
criteria may exist. In the simplest case, these relationships introduce
conditionality (IF - THEN) into the utility functions. In the worst case,
they necessitate recategorization of evaluation criteria as a function
of the values that one or more other criteria take on (van
der Smagt and Lucardie 1991, p.296). Other authors object to the validity
of the information which serves as input for algebraic utility functions,
in particular the determination of attributes and weights. They point out
that many of the techniques used to collect this information, especially
scaling techniques (Hourihan 1979; Burnett 1982;
Rhodes and Stern 1993), cause "intrusion of the method into the results"
(Pawson 1982, p. 54).
Alternative techniques for
modeling these complex types of interactions, such as decision plan nets
(Timmermans and van der Heijden 1987; Op `t Veld
et al. 1992) or relational reconstruction of choice sets (Reitsma
1990; Lucardie 1994) avoid some of these criticisms but they imply
increased model complexity, problematic data collection and few opportunities
for aggregation.
A pragmatic way out of this
morass of methodological controversy would be to not try to (re)construct
people's utility functions a priori, but instead allow them to freely formulate
their own; algebraic or conditional, locale-specific or spatially aggregate,
weighted or non-weighted, a priori or ex-post. This, however, requires
a very flexible representational scheme for utility functions and supporting
data model and software.
Rivers and reservoir systems have been modeled as networks of discrete
entities such as reservoirs, power plants, reaches, diversions, and so
on (Sigvaldason 1976; Labadie and Shafer 1979; Martin
1981; Loucks et al. 1989; Palmer et al. 1993). With the
recent advance of object-oriented programming techniques (Coplien
1992; Ellis and Stroustrup 1990; Lippman 1991) computer-based application
of this kind of model has been greatly facilitated. Object-oriented programming
provides a data model, the "object" model, which exhibits close correspondence
with discrete object structures or discrete event processes. In an object-oriented
model, object behavior consists of transitions from a state at time
t to a state at time t+1, where the transitions are a function
of the application of a dynamic D, invoked by the object itself,
typically in response to a message received from another object causing
a state change (equation
3).
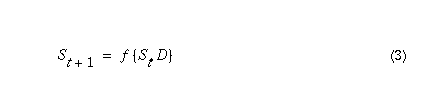
Applied
to a river basin, river basin objects such as reservoirs, confluences,
diversions, etc. are always in a particular state as expressed by the configuration
of their variable and parameter state data. An object's state changes by
receiving information; for example, an inflow, from another object. As
a consequence, it might apply a dynamic; for example, mass balance (Chapra
and Canale 1985), which further modifies its state. Certain state changes
induce the object to send a message to another object. For instance, when
an object computes its outflow, it may transfer that outflow to its downstream
neighbor where it is received as inflow. Likewise, calculated inflows representing
"requests" for water may be transferred to upstream objects. The cascading
of information through the network of objects (the river system) continues
until no more state changes occur. Then, the network is once again in balance,
and the simulation may proceed to the next time step. Whereas previously
complicated data models and control structures where necessary to manage
both the state data and the dynamics, object orientation provides a data
model through which both are maintained by the objects themselves rather
than by an overall, system-wide control component. Similarly, rather than
having some control component transfer information from one object to the
next (e.g., outflow-inflow fluxes), the objects simply send and receive
messages to and from each other. Although each object behaves autonomously,
collectively this behavior models that of the river as a whole.
This type of model is essentially
directionless in that information "flows" between objects in the direction
of the variables that need to be solved for. As such, the network structure
of objects is independent of whether a model is supply- or demand driven.
Which variables are solved for is exclusively a function of how the objects
are equipped with data; topological sorting of the network is not necessary
(Behrens 1994; Reitsma et al. 1994; Zagona
et al. 1995).
To facilitate modeling,
object classes can be equipped with libraries of dynamics or methods, of
which individual instances can be selected by users. For instance, reservoir
objects can be equipped with several methods for computing tailwater, evaporation
or elevation-area-storage relationships. Construed this way, all that is
needed to construct river basin models are the following:
-
A collection of generic objects representing the different components of
a river.
-
A user interface for (interactive) construction of the networks of objects
representing the river as a whole, loading of the data, setting up model
runs, inspection of model results, etc.
-
A queuing or parallel processing control component for managing the logistics
of the objects' state transitions and information exchange.
-
Data representing the objects' initial states.
-
Data representing the model's forcing functions (e.g., release schedules).
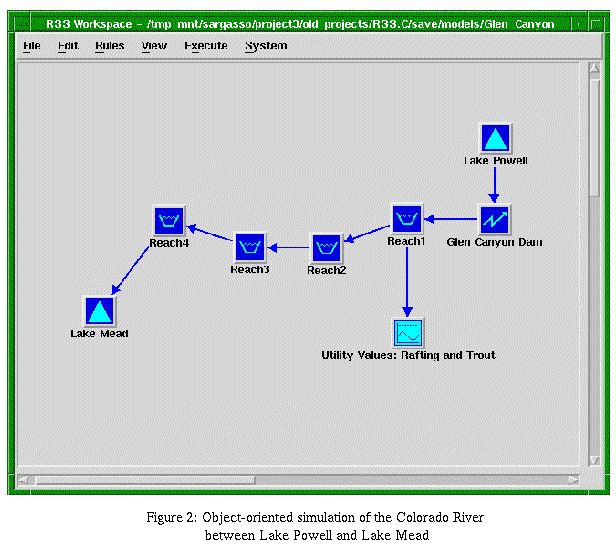 Figure
2 Object-oriented simulation of
the Colorado River between Lake Powell and Lake Mead
Figure
2 Object-oriented simulation of
the Colorado River between Lake Powell and Lake Mead
Figure
2 contains an example of a simple model constructed in this manner.
It represents a section of the Colorado River from Lake Powell to Lake
Mead. The dark, solid objects represent the hydraulic components of the
river. Water from Lake Powell is used for the generation of electricity
at Glen Canyon Dam, and then flows through Glen and Grand Canyons, represented
by a series of river "Reach" objects, into Lake Mead. Large scale applications
of this modeling technique are presented in Zagona
et al. (1995) and Eschenbach et al.
(1995).
This type of object-oriented process model can be extended to include plan
evaluation. If one considers plan evaluation merely as additional processing
of state data, there is no reason not to store this processing information
as well as its results, on the same objects that model the physical behavior
of the system. Integrating the physical process model with plan evaluation
models this way generates various advantages:
-
Since the objects maintain their own state and dynamics, any overhead associated
with communicating data between different data processing models (simulation,
plan evaluation) is no longer necessary. The logistics problems mentioned
earlier disappear;
-
Since evaluation computations become part of the behavior of the objects,
all computations for resolving the network, including the evaluations,
are conducted as part of a single computational process. The distinction
between physical process modeling and evaluation modeling, at least from
a computational or data model perspective, disappears;
-
Evaluation on the object model provides an elegant means for conducting
locale-specific evaluations. When evaluations are carried out by objects,
the evaluations are by definition localized and no topological or spatial
information must be duplicated on the side of the evaluation model;
-
Evaluation on the object level provides means for more ad hoc, interest-specific
plan evaluation. With the addition of an interpreted language for the definition
of utility functions, interactive, ad hoc definition of utility functions
becomes rather straightforward.
In the next section, we explore
the validity of the above claims through the application of the technique
on the simulation and evaluation of Colorado River streamflows.
The Colorado River (Figure
3) is one of the major water resources in the Western United States.
With a drainage area of approximately 632,000 square km and an average
annual natural flow of 18,132 million cubic meters, the Colorado River
provides water to seven states (CO, WY, UT, NM, CA, AZ and NV) as well
as parts of Mexico. The section of the river from Lake Powell to Lake Mead
(Figure
2), which includes Grand Canyon National Park, represents a complex
management situation, with numerous users competing for and impacting

Figure
3 Colorado
River Basin
the same limited resource. As witnessed by the U.S. congressional mandates
for this and other Colorado River projects, the initial operational objectives
of Glen Canyon Dam were aimed primarily at stimulating the regional economy
(water delivery and power generation) and providing protection against
floods and droughts. Recently, growing pressure from an increasingly varied
set of interests prompted a re-evaluation of the riverine resources and
of the Glen Canyon Dam and Lake Powell management objectives. Traditional
objectives such as water delivery, power generation, and flood and drought
control are now considered jointly with recreational, aesthetic, and environmental
needs (NRC 1987; USBR 1993).
For this study, the model of Figure
2 was extended with a series of small models for evaluation of alternative
reservoir release schedules. Five objectives, generally recognized as important
considerations in operating the canyon were selected: power generation,
river rafting, maintenance cost for recreational facilities, trout spawning
habitat, and habitat suitability for the humpback chub, an endangered species
of native fish (NRC 1987; USBR 1993). Criteria
for measuring the degree to which these objectives are realized under different
flow scenarios were defined in accordance with the results of a series
of environmental impact studies previously conducted on the operations
of Glen Canyon Dam (Bishop et al. 1988; Angradi
et al. 1992; USBR 1993). For instance, to evaluate the utility
of the river for white water rafting, the following empirical, second order
polynomial utility function (equation 4) was derived from results presented
by Bishop et al. (1988):
Y = 214.88 + 65.346X + .96126X²
(4)
where:
Y: surplus value for commercial rafting trips in
Grand Canyon National Park, and
X: average daily flow in cubic feet per second
(cfs).
The function is conditional in that only flows greater than 5,000 cfs
generate utility.
Humpback chub spawning utility
was defined in accordance with the findings by Angradi
et al. (1992) and USBR (1993). The
utility is normalized between 0.0 and 1.0, with 1.0 describing perfect
raising conditions of 5,000 cfs or lower flows, and 0.0 being a theoretical
minimum under conditions of infinitely high flow. Utilities are conditional
in that they are only to be computed for flows higher than 5,000 cfs, and
only during critical spawning periods (July - September).
Unlike humpback chub spawning utility,
trout spawning utility varies with locale. For instance, based on the studies
mentioned earlier, trout spawning utility in the Glen Canyon Reach was
defined as an empirical function of the percentage of redds continuously
submerged:
Y = 1 - (87,000 + 37.0X + 0.009X²) / 100
(5)
where:
Y: trout spawning suitability index.
X: minimum daily flow in cubic feet per second
(cfs).
This utility, however, is
only valid between October and May, and for flows under 15,000 cfs. Outside
this period, and at flows greater than 15,000 cfs, the objective is not
evaluated. For reaches other than the Glen Canyon Reach, a simple minimum
flow requirement of 2,000 cfs is sufficient as at those flows trout can
gain access to tributary streams where spawning can occur. Criteria for
the other objectives were defined in a similar way. Note that, quite deliberately,
no attempt was made to aggregate the various criteria into one, encompassing
utility index. Given the plurality of objectives, the very different interests
associated with them, and the legislative and political environment in
which these objectives are evaluated and administered, each of the interests
and their associated criteria were formulated independently and evaluated
against the physical behavior of the river.
5.2.
Model Specification
Table
1 summarizes the mappings of the hydrologic processes, policies and
plan evaluations on the one hand and their representations in the object-oriented
network model on the other.

The hydraulic part of the
model is constructed by interactively creating the various objects and
linking them together into a network representing the river. Three alternative
release schedules, representing typical releases under low, normal and
high flow years, were specified on the Lake Powell object. These are defined
as timeseries data, and loaded into the object's outflow variables. Initial
conditions are represented as scalars. Parameter data (e.g., head-area-volume
relationships and time lag coefficients), are represented as tables. Variables
representing the evaluation functions were defined through: (a) interactive
creation of additional state variables to store the evaluation results
on the objects, and (b) a simple "rule" language
for definition of conditional evaluation functions. This rule language
follows a simple syntax:
POLICY <policy name> TO_DETERMINE <variable name>FOR <object name>
BEGIN
IF <conditions>
THEN <result>
END
For instance, the definition of humpback chub rearing
utility was defined as:
POLICY chub_rearing TO_DETERMINE chub_rearing_utility FOR Reach
BEGIN
IF now() > June AND now() < October AND
Reach.flow > 5000
THEN chub_rearing_utility = 5000/Reach.flow
END
Trout spawning utility for Reach1 was defined as:
POLICY trout_spawning1 TO_DETERMINE trout_spawning_utility FOR Reach1
BEGIN
IF now() < May AND now() > October AND
Reach1.flow < 15000
THEN trout_spawning_utility = 1.0 - (87.0 + (3.7E-03)
Reach1.flow -(9.0E-07)(Reach1.flow)2)/100.0
END
For all other reaches, trout spawning utility was defined
as:
POLICY trout_spawning2 TO_DETERMINE trout_spawning_utility FOR Reach
BEGIN
IF now() < May AND now() > October AND
Reach.flow > 2000
THEN trout_spawning_utility = 1
END
The
above rules for trout spawning illustrate the use of object orientation
in considering the aspect of locale. Whereas trout spawning utility for
Reach1 is based on a specific empirical relationship, a more general utility
function is defined on the higher class level of reaches in general. Since
object-specific rules take precedence over class-specific rules, the Reach1
object always applies its own trout_spawning_utility rule first. If, for
any reason, all object-specific rules fail; i.e., the IF parts of the rules
all evaluate to FALSE, the object attempts the application of the rules
for its class. Reaches other than Reach1 only apply the more general rule.
Rules for evaluating the utility for rafting as well as for the other objectives
were formulated in a similar fashion. Finally, a generic output plotting
object (Figure
2: "Rafting and Trout Utility Values") was defined to collect and plot
all evaluation results from Reach1.
Running the model, now equipped
with several evaluation models, does not require any additional transfer
of data or locational information. As the objects perform their state transitions,
they now not only compute states associated with their physical processes,
but also evaluate their utility functions. Physical process modeling and
evaluation have been reduced to simple state transition functions under
a single data model: the object.
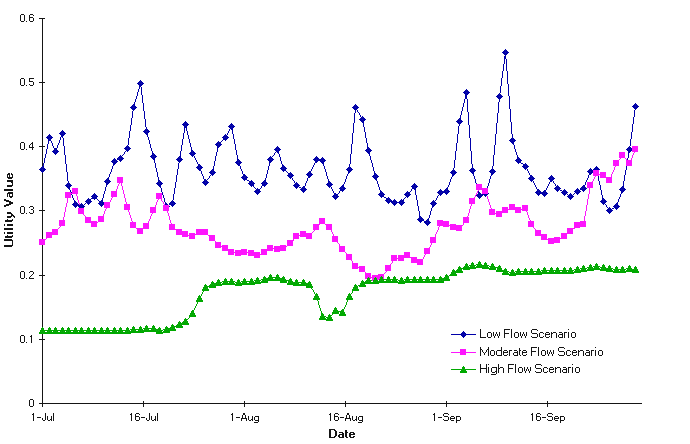 Figure
4 Utility Values for Humpback Chub Rearing Habitat
Figure
4 presents the results for humpback chub rearing for Reach1 under the
three different flow scenarios. They indicate that the mainstem Colorado
River does not provide good rearing habitat under any of the three flow
regimes simulated. During the critical rearing summer months, utility values
vary from a low of .11 (high flow) to .40 (low flow). Apparently, under
flow regimes other than a natural one where flows are well below current
operational guidelines, the young chub are under stress.
Figure
4 Utility Values for Humpback Chub Rearing Habitat
Figure
4 presents the results for humpback chub rearing for Reach1 under the
three different flow scenarios. They indicate that the mainstem Colorado
River does not provide good rearing habitat under any of the three flow
regimes simulated. During the critical rearing summer months, utility values
vary from a low of .11 (high flow) to .40 (low flow). Apparently, under
flow regimes other than a natural one where flows are well below current
operational guidelines, the young chub are under stress.
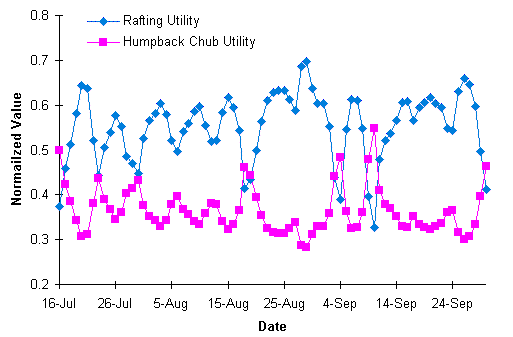 Figure
5 Utility Values for Rafting and Humpback Chub
Figure
5 Utility Values for Rafting and Humpback Chub
|
Since the evaluation functions
are interest-specific and defined independently, comparing evaluation results
provides insights into potential conflicts between objectives.
Figure 5, for instance, shows the evaluations for both humpback chub
rearing and rafting for an average flow scenario. The curves suggest that
under such a scenario the rafting objective is satisfied much more closely
than humpback chub rearing (both are expressed on normalized scales). The
curves show a virtually perfect inverse correlation (r < -.99), indicating
that what is good for the rafters is bad for the chub, and vice versa.
Although this example of analysis of conflict between multiple objectives
is rather simple, the concept offers interesting opportunities for more
complex types of analysis. For instance, in a paper on environmental modeling
and collaborative decision making, Carver et al.
(1996) argue for an iterative version of this technique whereby interests
are independently adjusted in search of windows of opportunity (= no conflict).
Traditional plan evaluation as part of environmental DSS often suffers
from a number of problems. Algebraic utility functions are often too simple
to represent the complexity of objectives and the various means of realizing
them. Conditions, locale, time-specific criteria definitions and the ways
in which definitions combine into an overall utility measure require flexibility
in defining evaluation functions. Moreover, many environmental decision-making
situations exhibit frequent changes in evaluation criteria as a function
of developments in the negotiation process, internal and external politics,
or new insights into how system variables are related to interests (Kaufman
and Duncan 1990). Not only must DSS be flexible enough to incorporate
those changes effectively, but the ad hoc nature of many of these changes
necessitates efficient means for doing so. This efficiency, however, is
hard to achieve using the traditional environmental DSS architecture where
all three system components (state information, process information and
evaluation tools) are represented by separate software and data models.
For instance, to support locale-specific utility functions, as in the case
of trout spawning utility, topological information about the network would
have to be represented both in the simulation model and the evaluation
software. Not only would this imply redundancy, but it would also mean
that every time the relationship between locale and utility changes, those
changes would have to be reflected in both models. The same argument can
be used in favor of bringing state and process information under a single
data model. Object-orientation offers attractive opportunities for developing
data models which unite all three components of environmental DSS.
Object orientation also
offers attractive opportunities for interactive, ad hoc definition of utility
functions. Since evaluations can be considered the results of merely processing
state data such as observational data and model forecasts, both the evaluation
computations and their results can be interactively expressed and stored
on either the river objects or on new, data processing objects. The latter
can then be linked into the network of river objects so that they will
conduct their computations as part of the larger simulation. This ad hoc
approach to evaluation has several advantages:
-
Evaluations can be interactively defined, modified and conducted by making
them part of the object network. Definitions can consist of simple algebraic
functions, but can also contain complex conditional relationships through
provision of an interpreted (programming) language which allows both computations
and conditional expressions;
-
Evaluations can be truly interactive and ad hoc. That is, users can define
new or alternative functions at any time during the modeling and evaluation
process. Since no data transfer between different software is necessary,
definition of utility is all that is needed. This makes real-time multicriterion
environmental decision making and negotiation a real-world possibility.
The Colorado River modeling
example illustrates that object orientation allows both state and process
information to be stored on objects where communication between objects
represent the fluxes within the environmental system. In addition, an object
that manipulates data to represent physical behavior can evaluate those
same data relative to one or more predefined objectives. Hence, all three
environmental DSS components reside at the object level. Locale-specific
definitions are easy to create since objects or groups of objects, by definition,
represent those locales. One simply attaches the appropriate evaluation
rules to those locales and runs the model. Many evaluations, each representing
different perspectives or "views" of an environmental resource, can be
computed simultaneously, and potential conflicts in space and time can
be explored by comparing the resulting utility profiles of various objectives
at any number of sites.
Angradi, T.R., Clarkson, R.W., Kinsolving, D.A., Kubly, D.M. and
Morgensen, S.A. (1992) Glen Canyon Dam and the Colorado River: Responses
of the Aquatic Biota to Dam Operations: Arizona Game and Fish Dept.; Phoenix,
AZ.
Behrens, J. (1994) Application of the PCRSS Reservoir Simulation
Model to the Salt River Project. In: Water Policy and Management, Solving
the Problems, edited by D.G. Fontane and H.N. Tuvel, New York, N.Y.:
American Society of Civil Engineers, pp. 295-298.
Bishop, R.C., Boyle, K.J., Welsh, M.P., Baumgartner, R.M. and
Rathbun, P.R. (1988) Glen Canyon Dam Releases and Downstream Recreation:
an Analysis of User Preferences and Economic Values. United States Bureau
of Reclamation, Glen Canyon Environmental Studies: Executive Summaries
of Technical Reports.
Bosman, A. (1983) Decision Support Systems. Problem Processing
and Coordination. In: Processes and Tools for Decision Support,
edited by H.G. Sol, New York, N.Y.: North Holland; pp. 79-92.
Brenner, M.J. (1973) The Political Economy of America's Environmental
Dilemma, Lexington, MA.: Lexington Books.
Burnett, P.K. (1982) Data Problems and the Application of Conjoint
Measurement to Recurrent Urban Travel. In: Proximity and Preference:
Problems in the Multidimensional Analysis of Large Data Sets, edited
by R.G. Golledge and J.N. Rayner, Minneapolis, MN.: University of
Minnesota Press, pp. 169-190.
Carver, S., Frysinger, S. and Reitsma, R. (1996) Environmental
Modeling and Collaborative Spatial Decision-Making: Some Thoughts and Experiences
Arising from the I-17 Meeting.
Proceedings of the Third International Conference/Workshop on Integrating
GIS and Environmental Modeling, held in Santa Fe, NM, January 21-26, 1996.
NCGIA, University of California, SantaBarbara.
http://www.ncgia.ucsb.edu/conf/SANTA_FE_CD-ROM/sf_papers/carver_steve/carver.html
Chapra, S.C. and Canale, R.P. (1985) Numerical Methods
for Engineers, Second Edition. New York, N.Y.: McGraw-Hill, Inc.
Cohon, J.L. (1978) Multiobjective Programming and Planning.
New York, NY.: Academic Press.
Coplien, J. (1992) Advanced C++. Programming Styles and Idioms.
Reading, Mass.: Addison-Wesley Publishing Co.
Dames K. and Moore J. (1993) Feasibility Study Report
for a Colorado River Decision Support System. Colorado Department of Natural
Resources and Colorado Water Conservation Board and Colorado Division of
Water Resources, Denver, CO.
Ellis, M.A. and Stroustrup, B. (1990) The Annotated C++ Reference
Manual. Reading, Mass.: Addison-Wesley Publishing Co.
Eschenbach, E.A., Zweifel, E.R., Magee, T.M., Grinstead, C.F. and
Zagona, E.A. (1995) Automatic Object Oriented Generation of Goal Programming
Models for Multi-Reservoir Management. In: Computing in Civil Engineering,
edited by J.P. Mohsen, New York, N.Y. American Society of Civil Engineers,
pp. 384-391.
Fedra, K. (1991) A Computer-based Approach to Environmental Impact
Assessment. IIASA RR, 91-13. International Institute for Applied Systems
Analysis (IIASA), Laxenburg, Austria.
Fedra, K., Weigkricht, E. and Winkelbauer, L. (1986) A Hybrid
Approach to Information and Decision Support Systems: Hazardous Substances
and Industrial Risk Management. In: IFAC Proceedings of the Conference
on Economy and Artificial Intelligence, Aix-en-Provence, France; pp. 169-175.
Fedra, K., Weigkricht, E. and Winkelbauer, L. (1993) Decision
Support and Information Systems for Regional Development Planning. IIASA
RR, 93-13. International Institute for Applied Systems Analysis (IIASA),
Laxenburg, Austria.
Finlay, P. (1994) Introducing Decision Support Systems, NCC
Blackwell; Oxford, United Kingdom.
Glasbergen, P. (ed.) (1994) Managing Environmental Disputes:
Network Management as an Alternative. Dordrecht: Kluwer Academic Publishers.
Guariso G. and Werthner, H. (1989) Environmental Decision
Support Systems, New York, N.Y.: Ellison Horwood Limited.
Hendriks, P.H.J. and van der Smagt, A.G.M. (1988) Definition
of Choice Sets and Choice Set Attributes, Some Problems Inherent in Decompositional
Modeling. In: Behavioural Modelling in Geography and Planning, edited
by R.G. Golledge and H.J.P. Timmermans, London: Croom Helm Publishing.
Hourihan, K. (1979) The Evaluation of Urban Neighborhoods 1:
Perception. Environment and Planning A, 11,1337-1353.
Kaufman, S. and Duncan, G.T. (1990) Preparing the Ground for
Mediation: Foothills Revisited. International Journal of Conflict Management,
1, 191-212.
Korhonen, P., Moskowitz, H. and Wallenius, J. (1992) Multiple
Criteria Decision Support - a Review. European Journal of Operational
Research, 63, 361-375.
Labadie, J.W. and Shafer, J.M. (1979) Water Management
Model for Front Range River Basins. Colorado Water Resources Research Institute,
Technical Reports; 16, Fort Collins, CO.
Lippman, S.B. (1991) C++ Primer, Reading, Mass.: Addison-Wesley
Publishing Co.
Loucks, D.P., Kindler, J. and Fedra, K. (1985) Interactive Water
Resources Modeling and Model Use: an Overview. Water Resources Research,
21, 95-102.
Loucks, D.P., Salewicz, K.A. and Taylor, M.R. (1989) IRIS. an
Interactive River System Simulation. Model, General Introduction and Description.
Cornell University, New York, NY, and International Institute for Applied
Systems Analysis (IIASA), Laxenburg, Austria.
Lucardie, L. (1994) Functional Object-Types as a Foundation
of Complex Knowledge-Based Systems. Rijswijk, The Netherlands: TNO
Bouw III.
Martin, Q.W. (1981) Surface Water Resources Allocation Model
(AL-V), Program Documentation and User's Manual. Austin, TX.: Texas
Department of Water Resources.
McLean, E.R. and Sol, H. (eds.) (1986) Decision Support
Systems: a Decade in Perspective. Amsterdam: Elsevier Science.
Nijkamp, P., Voogd, H. and Rietveld, H. (1990) Multicriteria
Evaluation in Physical Planning, New York, N. Y.: Elsevier Science
Publishers, .
NRC (National Research Council) (1987) Committee to Review the
Glen Canyon Environmental Studies River and Dam Management: a Review of
the Bureau of Reclamation's Glen Canyon Dam Environmental Studies, National
Academy Press, Washington, DC.
Op 't Veld, D., Bijlsma, E. and Starmans, J. (1992) Decision
Plan Nets and Expert System Tools: A New Combination for Application-oriented
Modelling of Choice Behaviour. The Netherlands, Journal of Housing and
Environmental Research, 7, 101-124.
Palmer, R.N., Keyes, A.M. and Fisher, S. (1993) Empowering
Stakeholders Through Simulation in Water Resources Planning. In:
Water Management in the '90s; A Time for Innovation, edited by K.
Hon, New York., N.Y.: ASCE, pp. 451-454.
Pawson, R. (1982) Desperate Measures. British Journal of Sociology,
33, 55-63.
Purdy, J.M. and Gray, B. (1994) Government Agencies as
Mediators in Public Policy Conflicts. The International Journal of Conflict
Management, 5, 158-180.
Reitsma, R.F. (1990) Functional Classification of Space; Aspects
of Site Suitability Assessment in a Decision Support Environment. International
Institute for Applied Systems Analysis. IIASA RR, 90-2. Laxenburg, Austria.
Reitsma R.F., Sautins, A. M. and Wehrend, S. C. (1994) RSS: a
Construction Kit for Visual Programming of River Basin Models. Journal
of Computing in Civil Engineering, 8, 378-384.
Rhodes, A.K. and Stern, S.E. (1993) Ranking Harassment: A Multidimensional
Scaling of Sexual Harassment Scenarios. The Journal of Psychology,
129, 29-39.
Rios, S. (ed.) (1994) Decision Theory and Decision Analysis:
Trends and Challenges. Boston, MA.: Kluwer Academic Publishers.
Sigvaldason, O.T. (1976) A Simulation Model for Operating a Multipurpose
Multireservoir System. Water Resources Research, 12, 263-278.
Sprague, R. and Watson, H. J. (eds.) (1993) Decision Support
Systems, Putting Theory into Practise; Third Edition; Prentice Hall,
N.J.: Englewood Cliffs.
Timmermans, H. J. P. (1986) Locational Choice Behavior of Entrepreneurs,
an Experimental Analysis. Urban Studies, 23, 231-240.
Timmermans, H. J. P. and van der Heyden, R. (1987) Uncovering
Spatial Decision Making Processes: a Decision Net Approach Applied to recreational
Choice Behaviors. Tijdschrift voor Sociale en Economische Geografie,
78, 297-304.
USBR (United States Bureau of Reclamation) (1993) Operation of
Glen Canyon Dam: Draft Environmental Impact Statement. Department of the
Interior, Bureau of Reclamation, Denver, CO.
van der Smagt, A.G.M. and Lucardie, L. (1991) Decision Making
Under Not Well-defined Conditions, From Data Processing to Logical Modeling.
Tijdschrift voor Sociale en Economische Geografie, 82, 295-299.
Zagona, E.A., Shane, R.M., Goranflo, H.M. and Waffel, D. (1995)
The INTEGRAL Project: The PRSYM Reservoir Scheduling and Planning Tool.
In: Computing in Civil Engineering, edited by J.P. Mohsen,
New York, N.Y.: American Society of Civil Engineers, pp. 210-217.
 JGIDA
vol.1, no.1
JGIDA
vol.1, no.1  JGIDA
Home
JGIDA
Home


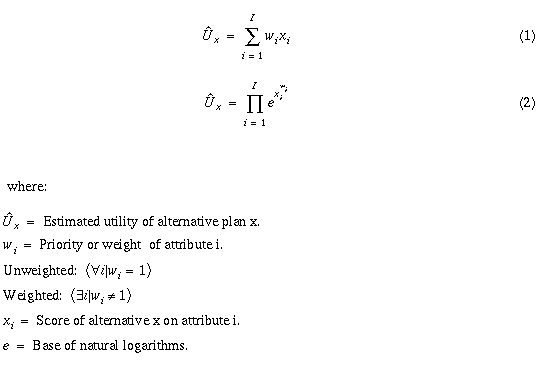
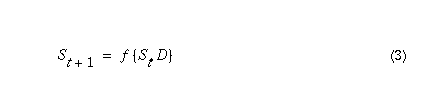
 Figure
2 Object-oriented simulation of
the Colorado River between Lake Powell and Lake Mead
Figure
2 Object-oriented simulation of
the Colorado River between Lake Powell and Lake Mead



