Bin Jiang
Centre for Advanced Spatial Analysis, University College London, 1-19 Torrington Place, London WC1E 6BT, UK
b.jiang@ucl.ac.uk
http://www.casa.ucl.ac.uk/bin/

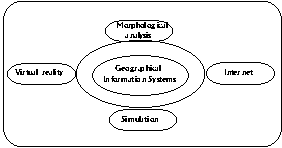
Figure 1  The framework of VENUE project

        The remainder of this paper is organised as follows. Section 2 briefly describes the model of multi-agent simulation and its link to urban environments. Section 3 is an overview of StarLogo, a computational tool for exploring self-organised systems. Section 4 introduces a representation of urban environments for urban morphological analysis. Section 5 details experiments on pedestrian movement in a virtual urban environment and analysis of the results. Finally section 6 summarises conclusions and proposes future work.
 

2. Multi-agent Simulation and Urban Environments
Multi-agent simulation is developed from the field of Distributed Artificial Intelligence (DAI). The baisc idea of multi-agent simulation is that programs exhibit behaviours entirely described by their internal mechanisms. By linking an individual to a program, it is possible to simulate an artificial world inhabited by interacting processes. Thus it is possible to implement simulation by transposing the population of a real system to its artificial counterpart. Each member of population is represented as an agent who has built-in behaviours. Multi-agent simualtion provides a platform to model situations in which there are large numbers of individuals and individuals have complex behaviours.
        The basic unit of a multi-agent simulation is the agent, where an agent is any actor in a system, any entity that can generate events that affect itself and other agents. Simulations consist of groups of many interacting agents. For instance, any ecosystem could consist of agents representing prey and predator respectively.
        Drogoul and Ferber (1994) have summarised multi-agent simulation as a set of the following elements: agents, behaviours, objects, environments and communications. Four of them are described by the quadruplet:

where agents are the set of all the simulated individuals, and behaviours are properties of agents; objects are the set of all represented passive entities that do not react to stimuli (e.g., buildings, street furniture in urban environments); environments are the topological space where agents and objects are located, where they can move and act, and where signals (sounds, smell, etc.) propagate; and communications are the set of all communication categories, such as voice, written materials, signs, etc.
        Applying the paradigm to urban systems, a couple of instances can be devised. Agents can be pedestrians and vehicles; Buildings, shops and museums are objects; The physical open spaces of the urban system can be regarded as environment; and communications can occur either between agents or between agents and their environments. Agents can be characterised by their behaviour in response to their environmental conditions and their neighbouring agents’ status. Thus communication could be considered in various ways, for example, a car sees another car close ahead, it may slow down; a tourist sees a direction sign, he/she may change their current heading. Human activities in urban environments are affected by the urban morphological structure (through the interaction between agents and environments) and by the status of neighbouring agents (through the interaction between agents).
        Multi-agent simulation has advantages over traditional numerical simulation techniques, which are based on mathematical or stochastic models, usually differential equations. Firstly multi-agent simulation provides impressive visual display with which users (simulation designers) can assess visually agents behaviour in the course of simulation. Secondly, users can dynamically trace how global structure emerge as a result of the agents’ individual interactions. One can use multi-agent simulation to test hypothesis, build up theories, and integrate different partial theories coming from various disciplines.
 

3. Self-organisation and StarLogo
There have been many efforts in providing software platform for multi-agent simulations. Swarm (Minar et al. 1996) is such a software platform, produced by Santa Fe Institute, for the simulation of complex adaptive systems. It is claimed to be a system that helps scientists focus on research rather than on tool building. In this respect, I believe that StarLogo (Resnick 1997) is exactly the kind of tool for scientists. It is developed from Logo as a programming language for children (Papert 1980).
        The idea behind StarLogo is so-called self-organisation, i.e. organised without an organiser, and co-ordinated without a co-ordinator. Orderly patterns can arise from location interaction between agents, and between agents and environments. The idea is not new as many computer models have such functions. Among others, cellular automata (CA) is probably the most influential in this respect. In CA, a virtual world  is arranged as a grid of "cells". Each cell holds a certain state, e.g. "alive" or "dead". Each cell is also assigned transition rules, for example, a cell becomes "alive", if the majority of its neighbouring cells are "alive", and in the same way a cell becomes "dead" if the majority of neighbouring cells are "dead".
         StarLogo has developed this idea, and incorporated three main types of characters in the virtual world: patches, turtles, and observer as in Figure 2. Turtles are the main inhabitants of the StarLogo world. Patches are the world in which the turtles live. Patches are arranged in a grid with the original co-ordinate in the centre. One can specify the size of patches and size of the environment according to the size of the turtles. If one likes to have the agents to look relatively realistic, then large patches are desirable. StarLogo can be regarded as a cellular-automata world with turtles roaming around on top. Both the patches and the turtles have a certain look, while the observer is invisible. Therefore it is like God, you cannot see it but it is there in the heart of believers. The observer is responsible for creating the turtles and patches and to monitor the activities of the turtles and patches.

 
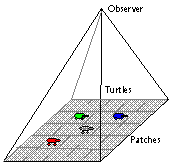
Figure 2  Three characters of StarLogo

        StarLogo is a programmable environment, and it provides a lot of procedures of patches /  turtles / observer to build up various applications, for instance, for creating turtles and defining the behaviour of turtles such as heading, movement and so on; for statistical analysis involving arithmetic functions; for visualisation like colour, data input / output and animation etc.. It also allows users to develop their own procedures.
        StarLogo language is a procedural language, and each procedure fulfills certain functions. The basic syntax is as follows:

<instruction> ::= <command-name> <expression>* | ( <command-name> <expression>* )

<expression>  ::= <operation-name> <expression>* | <list> | <quoted-word> | <number> |
                  <variable-ref> | ( <expression> )

<list>        ::= [ <list-element>* ]

<quoted-word> ::= " <word>

<list-element>::= <list> | <word>

<word>        ::= <string of characters other than space or [ or ]>

<variable-ref>::= : <word>

Except that there is also infix arithmetic with + - * / = < > in the usual way. Using StarLogo, one can produce applications with a friendly Graphic User Interface (GUI) linking to individual procedures, e.g. a button named "setup" links to a procedure "to setup". In the graphics window, one can watch the emerging patterns. Thus StarLogo provides innovative computational tools for exploring complex dynamic phenomena.
        Now let's examine how StarLogo fits into the basic principle of multi-agent simulations as described above. First of all, turtles are the basic agents. In addition, breeds are alternative agents in case more than one type of agent are needed. For instance, one might want foxes and rabbits in an ecology model, or antibodies and antigens in an immunology model. Secondly, objects in the StarLogo virtual worlds are identified by the location (x, y). Thirdly, patches are environments, which are usually identified by colours. For instance, if a road is coloured by grey, it can be used to limit a virtual pedestrian wandering around in the road. Finally, communications are achieved through the procedure ask (who, what), and they occur between turtles, between turtles and patches, and between patches and patches.
 

4. A Representation of Urban Environments
The structure of the environment that agents live in is of importance for studying self-organised patterns. Here an approach to the representation of urban environments is presented by concentrating on open spaces. The approach is termed as space syntax, which has a long tradition in urban studies (Hillier and Hanson 1984, Hillier 1996). More recently it has been brought to the GIS community as the potential for new functionality for spatial analysis (Jiang 1998, Jiang et al. 1999).

 

Figure 3 An urban environment and its axial representation

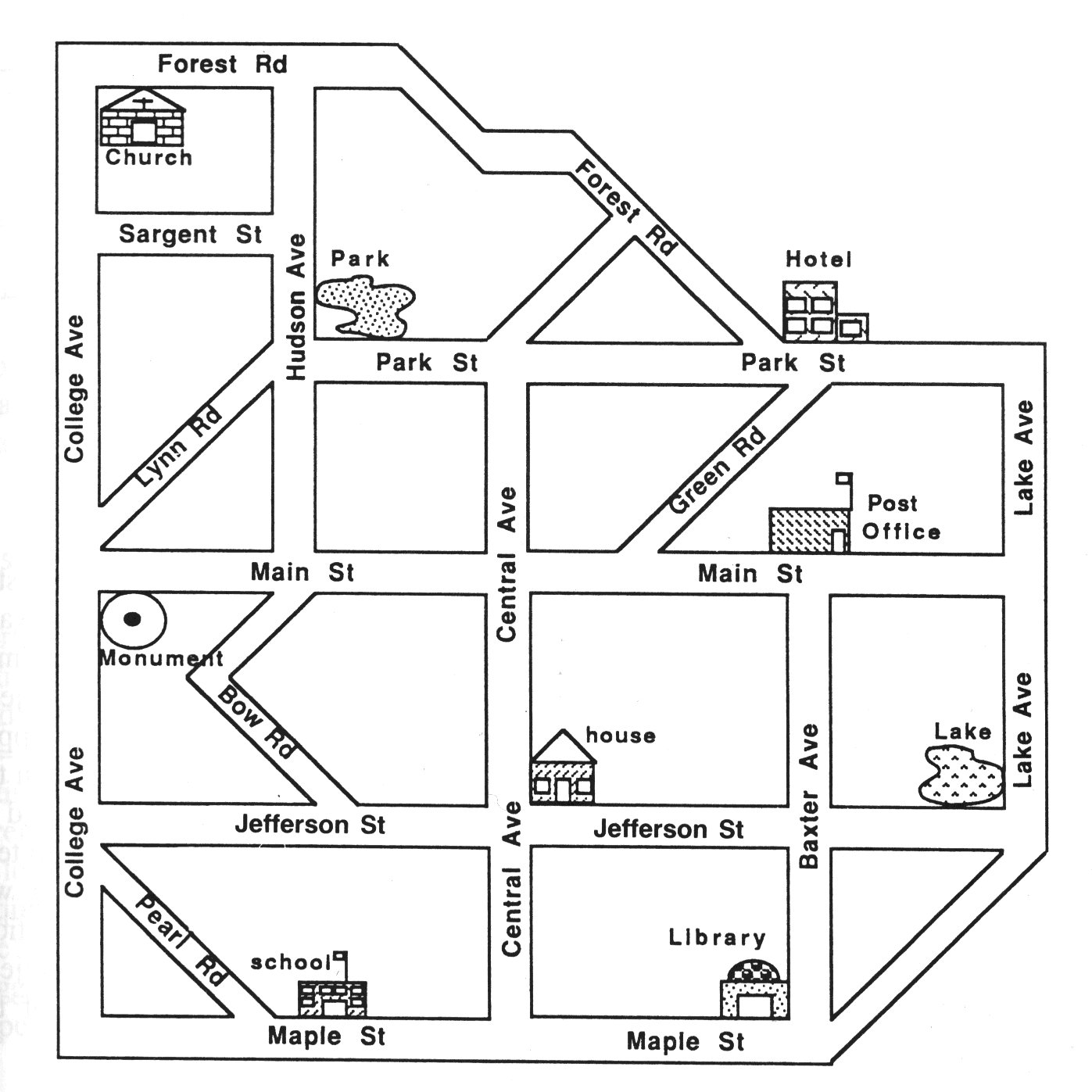
        Having a look at the urban system on the left in Figure 3, the open spaces are all interconnected, and one can travel from any point to any other point. It is this kind of characteristics that gives space syntax its unique position in modelling urban environments. One of the space syntax approaches is to represent open space as the longest straight lines. The whole urban system is crossed with the least number of longest axial lines, producing so called axial map (the model on the right in Figure 3). Taking each street segment as a node and each intersection as the edge, a related graph can be created. Based on the graph, a range of morphological parameters are derived. Among others, the following are important:
 - the connectivity C_j  of a line i is defined as the number of lines connected to that line. In the derived graph, it is equal to the number of nodes directly linked to each individual node;
- the control value crtli of a line i is defined as a measure expressing the degree of choice each line represents for its immediate neighbours as a line to move to, it is defined as

       and 

5. SimPed: Simulating Pedestrian Flows in a Virtual Urban Environment
As mentioned, the basic hypothesis to test is whether morphological structure has some impact on pedestrian movement in urban environments. To achieve this goal, a virtual urban environment with virtual humans is constructed using mulit-agent simulation. Such virtual worlds offer many advantages (Resnick 1997). In virtual worlds it is easy to create large number of virtual humans, it is easy to give new sensory capabilities to the humans, and it is easy to set up and control precise experiemental conditions.
        In this particular virtual world, a set of instances corresponding to the elements of multi-agent simulations is designed (Table 1). Agents are pedestrians with the behaviours of speed, heading and movement; objects are churches, hotels, monuments, post offices etc.; the physical urban space looks rather regular consisting of 21 streets as shown in Figure 3. The simulation (SimPed) is built upon StarLogo as introduced in the previous section.

 

Table 1  A set of instances in the SimPed Elements of multi-agent simulations Instances Agents pedestrian  behaviour:      speed (up | down)      heading (0-360)      movement (forward | backward) Objects church, hotel, monument, post office, school, library, park etc. Environments urban space with 21 streets in figure 3 Communications between red people  between red people and the urban environment

Figure 4 A snapshot of the simulation in progress (pedestrians moving randomly)

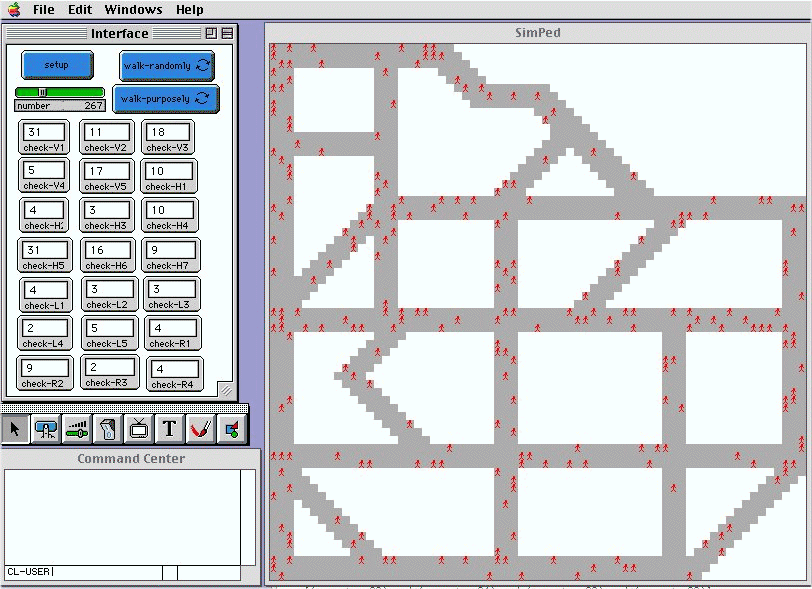        The simulation consists of two parts as shown in Figure 4. The right hand is a graphic representation of the virtual urban environment, within which pedestrians are pictured as red. The left hand is the control panel. The setup button creates the number of pedestrians walking in the urban environment. There are two continuous walk button namely walk-randomly, and walk-purposely. These two buttons set two different modes of the simulation. The former is random movement, while the latter is purposing movement, which means pedestrians have set destinations to reach. In addition, a set of monitor tools are used to dynamically record pedestrians every moment in each street for analytical analysis. Behind what you see on the screen is a range of procedures which keep the simulation running.  The following are some key procedures

to setup
  die
  setpedestrians number
  stopwalk-button
end

To check-no-kerb
  if (pc-at dx dy) > 6
    [seth (45 * random 8)
     check-no-kerb
    ]
end

to move-pedestrian
  if 0 = random 8
   [set (45 * random 8)]
 check-no-kerb
 jump speed
end

to check-street1
  output count-turtles-with
   [(xcor >= -33) and (xcor <= -31) and (ycor >= -33) and (ycor <= 33)]
end

to walk-randomly
  ask-pedestrian
   [move-pedestrian
    wait 0.1]
end

to walk-purposely
ask-pedestrian
  [ if who mod 9 = 1
   [setheading towards-nowrap -30 31]
   ;; to church
  [ if who mod 9 = 2
   [setheading towards-nowrap 15 14]
   ;; to hotel
......
end

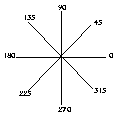Figure 5   Eight directions

        For the random movement mode, it is set that each pedestrian is initialised to head in one of eight directions (Figure 5), in the street layout. Once pedestrians come to a street crossing, they randomly choose the next heading, which is one of the eight. The total number of pedestrians within the virtual urban environment is changeable using the scale bar for investigating the overall pedestrian pattern. This type of simulation is called the aimless pedestrian, for example tourists. The result of the experiment has turned out to have a significant correlation (Figure 6) between pedestrian movement  rates and local integration obtained from space syntax analysis.

Figure 6 The regression plot between local integration and pedestrian movement rates
 

        For the mode of purposing movement, we have set all pedestrian destinations such as church, hotel etc.. The speed of each individual is set as a normal distribution, according to the existing observations on pedestrian movement (Helbing and Molnar 1997). However, it seems that there does not exist a significant correlation between pedestrian movement rates and local integration, particularly when time runs for a sufficiently long period. All pedestrians tend to cluster in their individual destinations (Figure 7). However, the final results seem not to be conclusive, as each pedestrian stops their journey once they have reached their destination. Further experiments are being carried out setting a range of destinations in a continuous course, that is, all pedestrians will continue their journeys with a further destination to reach, and thus they will never stop or cluster around certain locations.

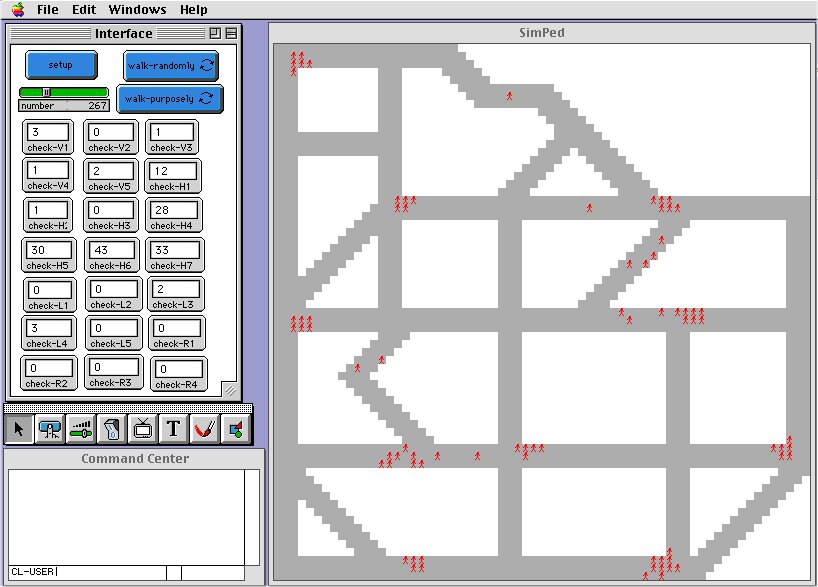
Figure 7  A snapshot of the simulation in progress (pedestrian moving purposely)

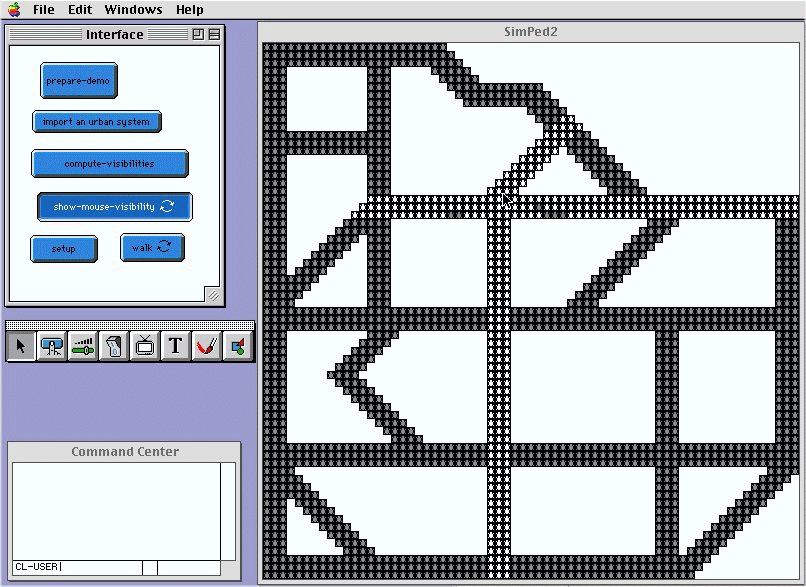
Figure 8  A visibility explorer

6. Conclusions and Future Work
This paper discusses some results about the experiments for pedestrian flows using a virtual urban environment. The experiments conducted are useful to illustrate some assumptions about human behaviour in urban environments. It has been shown that multi-agent simulation provides a valuable tool for urban environment simulation. Particularly in the experiments reported here, it has been found that urban morphological structures do have striking impacts on pedestrian movement in urban environments although this needs more work. Such simulations are useful for urban practitioners to assess draft urban plans, and also valuable for psychologists and geographers to study human behaviour in urban environments. The simulation capability can be further incorporated into GIS to be a new functionality for dynamic modelling.
         The experiments so far are based on a kind of local interaction, that is, the virtual pedestrians can only see one step ahead. However, they clearly show that simple local interactions lead to coherent patterns. From the point of view of modelling human behaviour in an urban environment, the work is not sufficient. We are carring on the work in attempt to give pedestrians a level of  global interaction. If pedestrians' sight is not limited to one step ahead, there is move of a global sense. In this connection we have designed a visibility explorer, with which one can explore visibility from any location within the urban environment. In Figure 8, visible sites from the mouse location are shown in white and the rests are shown in grey. With the visibility explorer, visibility becomes a property of each patch which can be transferred to pedestrians moving around. Thus, pedestrians movement can be based not only on local interaction, but global interaction as well.

References
Allen P. M. (1997), Cities and Regions as Self-organising Systems: Models of Complexity, Gordon and Breach Science Publishers: Amsterdam.

Batty M. and P. Longley (1994), Fractal Cities: A Geometry of Form and Function (San Diego: Academic Press).

Batty M., Dodge M., Jiang B. and Smith A. (1998), GIS and Urban Design, in Geertman S., Openshaw S. and Stillwell J. (eds.) Geographical Information and Planning: European Perspectives, in press, Springer-verlag, 32 pages.

Batty M. and Xie Y. (1997), Possible Urban Automata, Environment and Planning B, Vol. 24, No. 2, pp. 175-192.

Borgers A. and Timmermans H. (1986), A Model of Pedestrian Route Choice and Demand for Retail Facilities within Inner-City Shopping Areas, Geographical Analysis, Vol. 18, No. 2, pp. 115-128.

Drogoul A. and Ferber J. (1994), Multi-agent Simulation as a Tool for Studying Emergent Processes in Societies, in Gilbert N. and Doran J. (eds.) Simulating Societies: The Computer Simulation of Social Phenomena, University College London Press: London.

Helbing D. and P. Molnar (1997), Self-organisation Phenomena in Pedestrian Crowds, in Schweitzer F. (ed.) Self-organisation of Complex Structure: From Individual to Collective Dynamics, Gordon and Breach Science Publishers: Amsterdam.

Hillier B. (1997), Space is the Machine: A Configurational Theory of Architecture, Cambridge University Press: Cambridge.

Hillier B. and Hanson J. (1984), The Social Logic of Space, Cambridge University Press: Cambridge.

Jiang B. (1998), A Space Syntax Approach to Spatial Cognition in Urban Environments, Position Paper for NSF-funded research workshop on Cognitive Models of Dynamic Phenomena and Their Representations, October 29 - 31, 1998, University of Pittsburgh, Pittsburgh, PA.

Jiang B., Claramunt C. and Batty M. (1999), Geometric Accessibility and Geographic Information: Extending Desktop GIS to Space Syntax, Computers Environment and Urban Systems, forthcoming. 

Minar N., Burkhart R., Langton C. and Askenazi M. (1996), The Swarm Simulation System: A Toolkit for Building Mulit-agent Simulations, http://www.santafe.edu/projects/swarm/.

Papert S. (1980), Mindstorms: Children, computers and Powerful Ideas, New York: Basic Books.

Resnick M. (1994), Turtles, Termites, and Traffic Jams: Explorations in Massively Parallel Microworlds, The MIT Press: Cambridge.

White R. and Engelen G. (1997), Multi-Scale Spatial Modelling of Self-Organising Urban Systems, in Schweitzer F. (ed.) Self-organisation of Complex Structure: From Individual to Collective Dynamics, Gordon and Breach Science Publishers: Amsterdam.