Journal of Geographic Information and Decision Analysis, vol. 3, no. 1, pp. 41-55, 1999
Modelling Commuter Trip Length and Duration Within GIS : Application to an O-D Survey
 
Marius Thériault
Centre de recherche en aménagement et en développement (CRAD), Université Laval, Sainte-Foy, Québec, G1P 7P4, Canada
Marius.Theriault@ggr.ulaval.ca

Marie-Hélène Vandersmissen
Centre de recherche en aménagement et en développement (CRAD), Université Laval, Sainte-Foy, Québec, G1P 7P4, Canada

Martin Lee-Gosselin
Centre de recherche en aménagement et en développement (CRAD), Université Laval, Sainte-Foy, Québec, G1P 7P4, Canada

Denis Leroux
Université du Québec à Trois-Rivières, C.P. 500, Trois-Rivières, Québec, G9A 5H7, Canada
Denis_Leroux@uqtr.uquebec.ca 

Contents 
1. Introduction   
2. Simulation needs and issues   
3. Modelling and simulation procedure   
4. Empirical results and discussion   
5. Conclusion   
References		 ABSTRACT  This paper presents a modelling and simulation procedure to evaluate optimal routes (minimising impedance costs) and to compute travel times for each individual trip of an OD survey database. Canadian postal codes provide accurate locations within street blocks for each trip beginning and end point. Using TransCAD GIS software, the procedure finds the best routes through a topological road network. Each road (link in the network) is characterised by a maximal speed related to the functional class of the road, to its location in rural or urban areas, and to the distance from the nearest school. Turn and transfer penalties govern movements at the intersections. Moreover, the procedure calculates the number of persons travelling on every road (network link) to estimate a traffic map which is used to detect topological errors in the network and to estimate traffic congestion. Simulation results are totally dis-aggregated, making them suitable to model the mobility behaviour of individuals and households. They are key inputs in procedures for evaluating impact of transportation on housing markets (accessibility and traffic noise). Their availability for urban studies enables comparison of travel patterns among specific groups of persons. This procedure adds value to costly survey data that are already available in many North American cities, and enable space-time analyses of individual’s activities. The entire procedure can be run efficiently using a Pentium-based PC, even with large sample size (more than 100,000 trips). Hardware and software implementation costs are low (about 15,000 US$), making the computation tool accessible to transportation agencies and small research projects. 
KEYWORDS: topological networks, optimal route  modelling, origin-destination surveys, geographical information systems, transportation studies.
1. Introduction
Travel time is among the most important factors that affects attractiveness of transport modes and consequent  commuter travel decisions in urban areas (Makin et al. 1997). Accurate estimates and comparisons of travel paths and the duration of trips are basic requirements for planners, transportation industries, marketing businesses and social scientists. Their applications must consider aggregated effects of individual choices on the market penetration of public transport facilities. They need models to evaluate the foreseeable impact of new residential developments on the long term evolution of road traffic. They must improve understanding of how people choose where to live, shop and pursue leisure. The need to consider how travellers trade off costs within temporal constraints, while keeping inconvenience to the daily life of their households within acceptable limits (Arentze et al. 1993; Miller 1991).
        This paper presents a procedure to model commuters' travel routes and transit times using a very large data bank on commuting trips recorded in an Origin-Destination (OD) survey. Its purpose is to enhance the evaluation of mass transportation demand and to permit geographical analysis of commuters behaviour. The immediate objective is twofold. Firstly, we need to overcome methodological issues in modelling huge number of travel routes. Secondly, we want to demonstrate the feasibility and fruitfulness of integrating sophisticated simulation procedure into existing and user-friendly geographical information system (GIS). The ultimate purpose is to design efficient tools for large scale simulation.
        Evaluating duration of commuting trips is a basic requirement for our research program. We want to understand and model the evolution of households' mobility in relation to the geographical accessibility of activities in the Quebec metropolitan area (Canada). This mid-size city has an over-developed highway network: 21.7 km per 100,000 inhabitants.
        OD surveys are the main source of data about urban mobility in Canada, and elsewhere in North America. However, while these surveys yield the usual zonal matrices, they offer little or no data on individually chosen paths, in terms of either distance or time, even though this information is indispensable for transportation planning, since trip duration and route geography are the most significant variables to consider while modelling commuters behaviour (Gordon et al. 1991).
        Gathering this crucial time information implies one of the following alternatives: 2. Simulation needs and issues
The last option, retained here, is a compromise between the calculation of Euclidean distances and the use of GPS or activity based surveys. OD data are used to estimate the most likely paths that minimise impedance costs for each commuter trip. This modelling procedure provides consistent estimates of journey duration and travelling distance using existing data. This is an absolute requirement to allow the retrospective study of the evolution of transportation within metropolitan areas.
        To be adopted by end-users (planners, transport analysts, economists, scientists), the proposed tool should be portable, user-friendly and accessible to small transportation agencies. The development of such decision support systems is one of the major challenges in the GIS community (Etches et al., 1998). They would exploit available OD data for the benefit of transportation agencies, businesses (accessibility assessment) and society as a whole (linkage among land uses and their effects on transportation).
        The main database used for this mobility analysis comes from the OD survey carried out by the Quebec Urban Community's public transportation corporation (STCUQ), in 1991. This survey (Table 1a) describes about 111,224 trips related to 50,808 persons (8% of the total population) living in 20,796 households. The geographical database of the road network (Table 1b and 1c) for the metropolitan area was topologically structured (Thériault et al. 1995); it contains 52,538 street segments (directional links) and 19,249 nodes.
        Generating 111,224 minimal cost paths to estimate travelling time and distance of each OD trip involves methodological and technical issues. Literature dealing with the shortest path calculation is well developed and efficient solutions have been put forward (Adamson and Tick 1991; Khoong 1993; Pearn et al. 1994). A classic solution, based on Dijkstra's algorithm, is already implemented in many GIS but requires, in the worst conditions, V2 steps (V = number of nodes) to reach a solution (Sedgewick 1990). Generating the 111,224 individual routes from the STCUQ OD survey could take 4.12 x 1013 (111,224 x 19,2492) steps. Even with a powerful computer system, that can mean days, probably weeks, of computing.
        On the other hand, to generate the most probable route in a network, knowing only the origin and the destination, one need to consider all possible network configurations for any transportation mode in the entire urban area: private cars, public transportation (bus routes and schedules), bicycle, pedestrian, etc. The value of expected results will mainly reflect the quality and completeness of the network database used for the calculation and impedance specification. For the Quebec network, this means adding an impedance coefficient to each of the 52,538 road segments to reflect travelling resistance according to road type (highway or local road for instance). This also implies providing a table in the network database for the identification of prohibited turns and for penalties related to moves at intersections. Furthermore, the OD pairs must be located in space and linked to the nearest road for route computation.
 
Table 1 OD survey and road network tables structure
(a) OD Trips Origin Destination Survey Trips (111,224 records in the 1991 OD survey)
Field Format  Step Content (units/procedure) [software] 
TripId Integer  OD Unique ID for each OD survey trip 
PersonId Integer  OD Unique ID for each respondent 
Origin_Pcode Char*6  OD 6 digits Canadian postal code at the starting point of the trip 
Destin_Pcode Char*6  OD 6 digits Canadian postal code at the ending point of the trip 
Mode Integer  OD Transportation mode {car; bike ... } 
Purpose Integer  OD Trip purpose {work; shopping ... } 
Expansion Integer  OD Expansion factor (computed for each municipality by respondents' age group and sex to estimate ratios between census counts and the OD survey respondents; used to expand OD trips to the total area population) 
Origin_Lat Real  PA Latitude of the origin (degrees) 
Origin_Lon Real  PA Longitude of the origin (degrees) 
Destin_Lat Real  PA Latitude of the destination (degrees) 
Destin_Lon Real  PA Longitude of the destination (degrees) 
Origin_Node Integer  NA Road network node (excluding highways) nearest to the origin location 
Destin_Node Integer  NA Road network node (excluding highways) nearest to the destination location 
Travel_Time Real  RS Total modelled travel time by car on the road network (minutes) 
Route_Length Real  RS Optimal route length (kilometres) 
 
(b) Road Links Road Network Links (52,538 records in the 1988 road network)
LinkId Integer  RD Unique ID for each road link 
LinkDir Char*2  RD Road link direction {AB : forward; BA : backward} 
Road_Name Char*40  RD Street/Road name 
Functional Integer  RD Functional class {street; local road; major road; regional road; national road; highway; highway exit} 
Speed Integer  RD Road link speed (kilometres per hour) [see Table 3] 
Length Real  RD Road link length (metres) [MapInfo] 
Time Real  RD Road link travel time (minutes) [MapInfo; Length*60/Speed*1000] 
Start_Node Integer  RD Starting node [TransCAD] 
End_Node Integer  RD Ending node [TransCAD] 
Traffic_Count Integer  RS Traffic count; sum of Expansion for every individual OD route using the road link (persons travelling on the segment during a typical weekday) 
 
(c) Road Nodes Road Network Nodes (19,249 records in the 1988 road network)
NodeId Integer  RD Unique ID for each network node 
Latitude Real  RD Node latitude (degrees) [TransCAD] 
Longitude Real  RD Node longitude (degrees) [TransCAD] 
Functional Integer  RD Maximal Road link functional class connected to this node {street; local road; major road; regional road; national road; highway; highway exit} [MapInfo; using geometric intersection with road links] 
 
(d) Postal Codes 6-digit Canadian Postal Code Locations (23,126 records in 1991)
(from Statistics Canada PCCF ; checked using Canadian Postal Corporation maps and the road network)
P_Code Char*6  PC 6-digit Canadian postal code 
Latitude Real  PC Postal code latitude (degrees) 
Longitude Real  PC Postal code longitude (degrees) 
 
        The geographical location of OD pairs uses Canadian postal codes (Table 1d), allowing resolution to the block face level (generally < 100 metres from real position) with 23,126 postal code locations.
Such geographical detail implies using GIS to manage spatial data, to update the road network, to operate the selection of the best route and to check for data correctness. To reduce processing time and to design a tool that could be run on a relatively cheap system, reasonable criteria sets and route computing procedures must be developed and/or integrated into the GIS package using their extension development languages. That is the specific purpose of this paper. We implement a modelling procedure for the Quebec region 1991 OD survey, using currently available commercial GIS packages running in conjunction with Windows 95, in order to test the feasibility of this approach with current technology and to evaluate its operational costs (processing time and/or money).
 
3. Modelling and simulation procedure
The modelling procedure is divided into six consecutive steps shown in Table 2. Figure 1 presents a general data processing flow chart making use of various software packages to relate and mutually enrich the four base tables. The first three steps are devoted to data gathering from multiple source documents. These data are often already available for many urban regions in North America and need only to be checked for their suitability and correctness. For the Quebec region, it was decided to rebuild or check the entire database to deliver maximum quality (cost estimates are provided in Table 2).

Figure 1  Data processing and simulation flow chart
             The first step (RD) was devoted to editing and building of a topological road network using 1:20,000-scale topographical maps (Figure 2). This accuracy level is mandatory to ensure future compatibility with GPS technology. This is a huge task that can be done using powerful GIS packages, like Arc/Info running on Unix platforms. For our project, in order to minimise equipment costs, we developed an add-on application (MapLogix) running in conjunction with MapInfo (MapInfo Corporation 1996) for Windows 95. It is now commercialised (Korem 1998). In a computerised road network, each link must contain appropriate identification and labelling of road segments (network links; Table 1-b) and street intersections (networks nodes, Table 1-c). Some links are unidirectional: this information was added to road segments using a custom-made tool programmed in MapBasic (MapInfo Corporation). To simulate the real world, each road segment (link) must be characterised by the speed it allows for various transportation modes (here we retain only private cars) and penalties may be specified for various movements at intersections (nodes). Adding exact information for each of the 52,538 road segments and 19,249 nodes in the network is nearly impracticable. Therefore we decided to use the functional classification of roads provided by the Quebec provincial Ministère des transports, adding three supplemental local criteria to enhance the local context’s impact on travelling speed (Table 3 and Figure 4). These criteria are compatible with legal speed limits and were implemented using MapInfo's Geo-SQL and updating capabilities. Together, they distinguish between highways, highway interchanges, rural and urban roads, and local streets with or without nearby elementary school. For the seek of simplicity, the intersection penalties were specified globally for the entire network using the appropriate option of TransCAD (Caliper Corporation 1996), the GIS software retained to model the route choices. This is not an absolute restriction, since TransCAD allows for many other methods, including site specific penalties. This set of criteria provides a realistic basis for simulation of route choices, matching the average behaviour of individuals travelling across the city (they minimise their travel time while avoiding complex paths). For the Quebec region, we do not consider road congestion, postulating that it seldom happens, due to the high density of its highway network.

 
Figure 2 Road network modelling
 Figure 2 Road network modelling
 
Table 2 Modelling procedure steps
Step Name  Procedure [software] (time and/or cost) 
RD
Road network creation
 Topological structuring of road links from 16 topographical 1:20,000 map sheets [MapInfo-MapLogix] ; Manual assignment of road directions, functional classes and names [MapInfo] ; Road network creation [TransCAD] (computer assisted procedure ; 32 weeks ; approximate cost 35,000 CAN$) 
PC
Postal code location
 Assign and check latitude and longitude co-ordinates for each 6 digits postal code in the region [MapInfo-MapBasic] (computer assisted procedure; 10 weeks; cost about 6,000 CAN$) 
OD 
OD survey
 Phone survey (computer assisted procedure involving 30 operators ; 8 weeks ; cost 250,000 CAN$, including phone calls) [Access-MapInfo] 
PA
Postal code assignment
 Assign postal code location (latitude and longitude) to each OD starting and ending points [MapInfo] (13,148 locations ; 25 minutes) 
NA
Nearest node assignment
 Assign nearest network node (excluding highway nodes) to each trip starting and ending points [MapInfo-MapBasic] (75 minutes) 
RS
Optimal route search
 Find the optimal route (minimising travel time) for each OD trip using the road network and table 3 criteria; update the OD trips table with travel time and route length ; update the road network links with traffic counts [TransCAD-GISDK] (722 minutes for route simulation and 9 minutes for road traffic updating) 
 
        The second step (PC) improves the geocoding (providing geographical co-ordinates of the starting- and ending-points of trips). In Canada, the postal code is used to locate individuals and households in space. In urbanised areas it provides location at the block face level. Statistics Canada maintains a conversion file (PCCF) that associates geographical co-ordinates (latitude and longitude) to each 6-digit postal code. Thus, the 6-digit postal code was retained to indicate every position within the OD survey (Figure 3). However, the precision of Statistics Canada's location is insufficient and incompatible with our accurate road network. Some postal code locations were even found in the middle of the Saint-Lawrence River at hundred of metres from any land. It was then decided to check the location of every postal code in the region using maps published by the Canadian Postal Service Corporation to put them in the appropriate street block (Table 1-d).
 
Figure 3 Location of the postal codes on the road map 
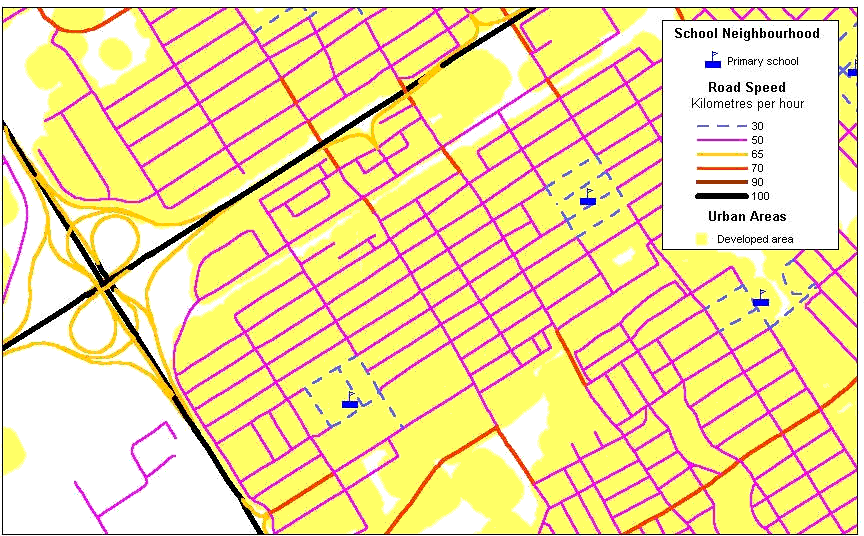
Figure 3 Location of the postal codes on the road map		 Figure 4 Assignment of maximum speed to every road link 
Figure 4 Assignment of maximum speed to every road link
 
        The third step (OD) implies the creation of a trip information table from the OD survey. Examples of necessary information fields coming from that operation are tagged with the "OD" label in the "Step" column of  Table 1-a. Remaining fields in this table are to be filled during upcoming data processing steps.
        The fourth step (PA) associates geographic co-ordinates coming from the postal codes location table to the starting- and ending-points of each trip (Table 1-a). This operation can be undertaken with any software that implements SQL join operations. However, GIS capabilities are needed to use latitude and longitude in order to generate point features that are needed at the next step, so it was appropriate to use MapInfo to handle this task.
 
 
Table 3 Speed and turn penalty assignment criteria for modelling of private car routes
(a) Speed Criteria used to assign speed to each road link in the network
Functional class
Additional criteria
Speed (km per hour)
Street within 150 metres from a primary school (>=100 pupils) 
30
Street at more than 150 metres from a primary school (>=100 pupils) 
50
Local road in urban areas and within 150 metres from a primary school (>=100 pupils) 
30
Local road in urban areas and at more than 150 metres from a primary school (>=100 pupils) 
50
Local road in rural areas 
70
Major road in urban areas 
50
Major road in rural areas 
70
Regional road in urban areas 
70
Regional road in rural areas 
90
National road in urban areas 
70
National road in rural areas 
90
Highway exit Ramps, exits, entrances, etc. 
65
Highway High speed divided lanes 
100
 
(b) Turn penalties Global criteria used to assign time penalties for specific movements at each network node using TransCAD
Movement
Time penalty (minutes)
Turn left
0.4
Turn right
0.2
Through
0.1
U-turn
prohibited
 
        The next step (NA) uses these point locations to find the nearest node in order to establish a geometric link between the OD survey and the road network. Despite that TransCAD provides an automatic function to handle this task, linking each point to the nearest node, it was decided to implement it in MapInfo, using a custom-tailored MapBasic program, in order to avoid increasing the complexity of the network resulting from several simulations. This program uses the buffering functions of MapInfo to select the nodes at increasing radial distance from every point, retain the nearest one and update the appropriate field of the OD trips table (Table 1-a), using its identifier. To prevent users from entering the network through an highway connector, these specific nodes were excluded from the table before node assignment. The Geo-SQL functions of MapInfo were extremely efficient to aggregate the "Functional" field of road links (Table 1-b) in order to qualify each node using the maximum value of every connected link (Table 1-c).
 
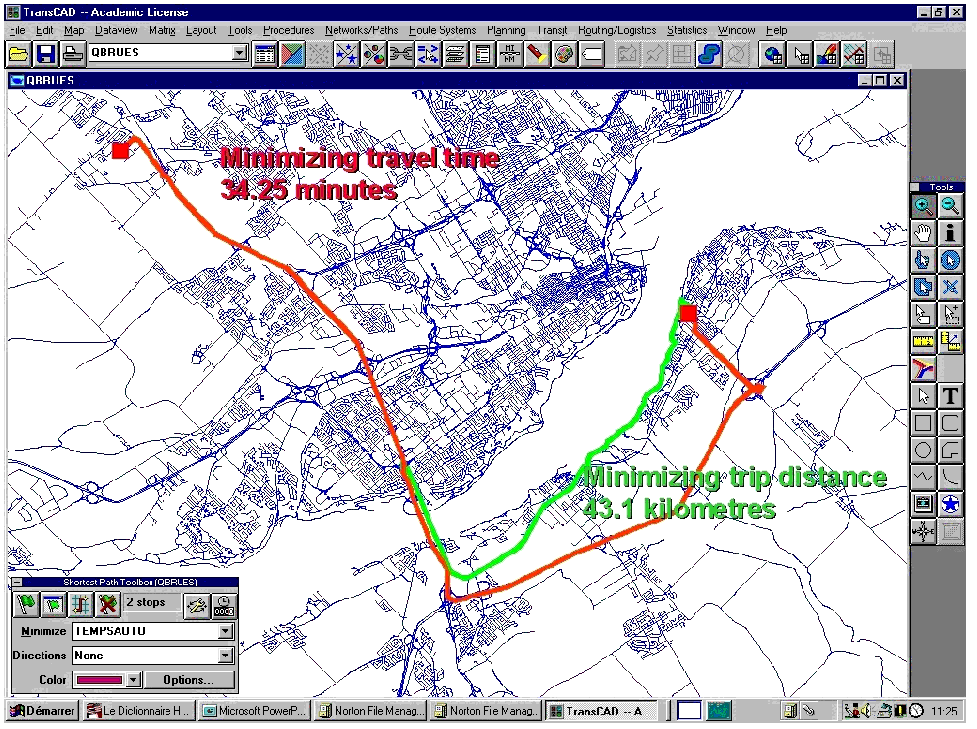
Figure 5 Finding optimal routes using TransCAD  
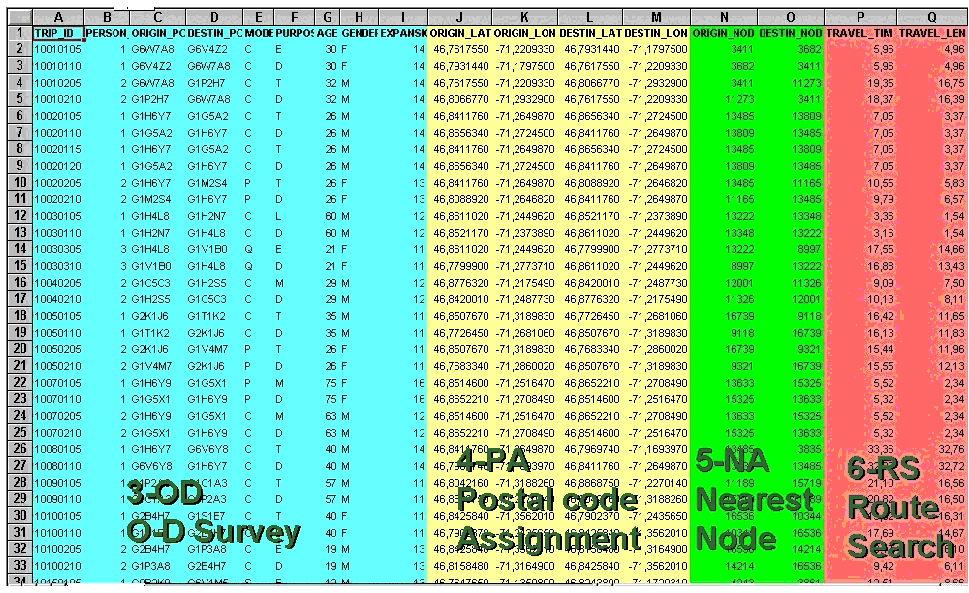
Figure 5 Finding optimal routes using TransCAD		 Figure 6 Adding trip location and statistics to an O-D survey table 
Figure 6 Adding trip location and statistics to an O-D survey table
 
         Finally, the last step (RS) uses TransCAD functions to find the optimal route for each OD trip (mainly the ShortestPath procedure). However, despite that TransCAD provides a very efficient user-interface to model trips directly on the screen (Figure 5), pointing locations on the network, and to model the entire matrix of routes between two sets of nodes, there is no function to handle a set of nodes taken from a file or a table. With thousands of routes to model, the first operation mode (pointing on the screen) was impracticable. The nodal matrix was also rejected because it implies building the entire 19,249x19,249 matrix to retain a mere 111,224 actual routes, rejecting 370,412,777 remaining cell results. Overload on resources (estimated at many weeks of processing time with a 200 MHz Pentium, needing more than 6 Gigabytes of disk space for storage) would clearly exceed any PC's capabilities for a while. Once again, it was decided to build a macro program using the GISDK (Caliper Corporation) language running in conjunction with TransCAD (Figure 7). This macro establish a direct link between the OD trip table, providing the route beginning- and ending-nodes of each journey, the road network and the criteria set (penalties, fields to minimise and update) to model the requested paths. These paths are then measured in length and travelling time to update the OD survey table (Table 1-a and Figure 6) and, optionally, to accumulate traffic on every link of the network (Table 1-b).
 
 
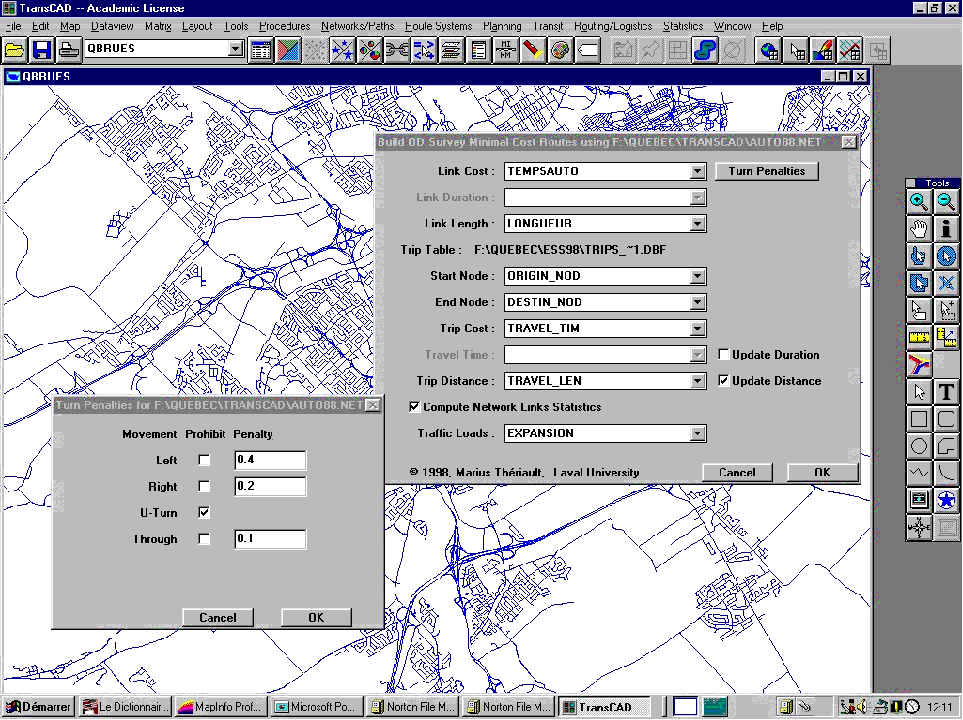
Figure 7 Procedure to update the O-D table with trip data 
Figure 7  Procedure to update the O-D table with trip data
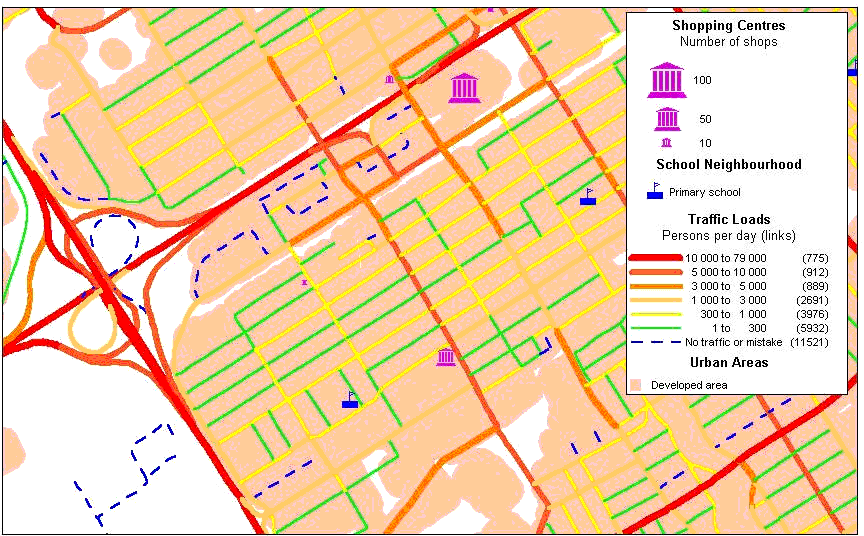
 Figure 8 Estimated traffic during a typical weekday 

Figure 8  Estimated traffic during a typical weekday: Example for Limoilou, Fall of 1991
 
        This last function is a side benefit: it does not slow down the procedure and implies only a small overload of about 10 minutes to record the traffic information for our entire network. The information gain is very significant: it transforms an OD survey into traffic maps that can be used to model road congestion and, when calibrating a new network, to disclose topological errors, since an inappropriately connected or inaccessible link will generally return a null traffic. It is an error detection tool that has clear advantage over the tedious manual checking of every connection in a topological network. It can even be applied without an OD survey, by choosing starting- and ending-nodes at random.

4. Empirical results and discussion
The main purpose of this project being to develop a tool adapted for small transportation agencies and low-funded research projects, it was decided at the very beginning to retain a PC platform using a conjunction of two low cost and widely available GIS packages, MapInfo and TransCAD, running on the popular Windows 95 or Windows NT platforms. These two packages are user-friendly and provide excellent interoperability features (ODBC, SQL relational principles, MapInfo interchange format to handle map and data transfers, extension through MapBasic and GISDK languages, etc.).
        Beyond specific simulations from our OD survey, the primary goal was to develop a procedure that can be re-used for various other purposes, such as modelling the time accessibility of services within a city, comparing the efficiency of two transportation modes, etc. Processing times (based on a 200 MMX Pentium PC with 96 Megabytes of RAM) are reported in Table 2, and can be useful to estimate the feasibility on any specific project using that procedure. While refining our approach, early processing time expectations, expressed in days or weeks, became hours, and even, minutes. However, we experienced some performance problems with the TransCAD route simulations. After some 80,000 routes had been found at a very impressive speed, the system performance gradually deteriorated showing excessive disk activity. After 90% of the overall modelling task was carried out in about 12 hours, activity reports displayed on the screen by our GISDK application indicated that about 1% of the remaining task took the next 10 hours. So, we decided to cancel the processing. The problem is probably related with overlays and data transfer between the RAM and the virtual memory that appears when the task is large and the available disk space becomes low. Thereafter, we decided to disable virtual memory swapping at the system level and to restart the application. The system performance then stay constant and the reported time of 722 minutes for route simulations appearing in Table 2 comes from this operation. Using memory swapping yields longer processing times, even for small tasks. TransCAD, as well as many other packages, seems relatively unstable without virtual memory and it is highly advisable to reset the system after the simulation results are secured to disk.
        A second test was conducted to model the same trips using a criteria set pertaining to travelling by bicycle: 20 km per hour, highways prohibited, time penalties of 0.2 minute for a left turn, 0.1 minute for a right turn, 0.4 minute for an U-turn, and 0.2 minute for a through movement. Providing ample disk space, the system performance was stable and the job took 1917 minutes of processing time. Part of the increase in computing time (1917 / 722) is related to greater complexity of each route; the number of links to pass through is larger when one has to avoid highways. Most shortest path algorithms are marginally sensitive to such increasing complexity.
        The first three steps in the modelling procedure imply fixed costs that must occur only once or at specific times for a region (generally during census, at 5 years intervals). That is where the higher investment burden is concentrated. In many regions, including North America, these data are currently available and the investment has already been made. The remaining three steps imply mainly operational costs that are very low when compared with the investment in data gathering. Furthermore, the added value of information is very high compared with the marginal operational  costs, clearly yielding benefits. Despite, its pitfalls if the sample size is too small, transforming an OD survey to estimate traffic at every point of a network is cost-effective when compared to that of operating a vehicles count to monitor  network over an entire region. Furthermore, simulation results can be calibrated using such real world measurements.
        This simulation procedure adds three important pieces of information to the OD trip table (travel time and route length) and to the road network (traffic count). These supplemental attributes may be associated with other pieces of information already in these data sets to generate detailed analyses of commuters behaviour. Future enhancements of our GISDK macro will enable the production of polylines associated with the physical route followed by each traveller and their export in a format compatible with GIS packages.
        Analysing the situation of the Quebec region in detail is far beyond the scope of this paper. The procedure must be extended to include specific methodologies to model public transit networks with schedules and transfer penalties before it becomes fully appropriate to model all transportation modes. However, Table 4 and Figure 8 give some examples of the type of information one may generate with subsequent statistical analysis and mapping operations using these data.
        Table 4 shows statistics based on aggregating travel time (minutes) and route length (kilometres) of all OD 1991 trips segmented by gender of the travelling person, trip purpose and transportation mode (car driver, car passenger and taxi passenger). Individuals using the bus system, biking or walking were excluded because the simulation criteria used are irrelevant to their situation. Table 4 reveals classical findings. Men do more trips to work than women mainly because they are more involved in the labour market. The proportion of trips made by women as car passengers (18%) is three times that of men. Men make longer trips to their work place (Johnston-Anumonwo et al. 1995; Blumen and Kellerman 1994). However, differences of travelled distance between genders (9.84 km versus 8.94 km) are becoming smaller than those of previous surveys. This could be an indication that travel behaviour of men and women is becoming more similar (Camstra 1996). Trips for shopping by passengers (car or taxi), are mainly made by women (84%), but the lengths of these trips are quite similar at 6.64 km and 6.36 km for women and men, respectively. Since OD data and road network are located in space, it is also possible to aggregate results by geographical areas such as municipalities, zones or census tracts. Then, aggregating trips in order to compare downtown and suburb locations would probably be useful to analyse differences between men and women in terms of trip length or home location decision (Preston and McLafferty 1997).  Figure 8 presents a zoom over a map of traffic density (persons travelling on each road segment). In MapInfo and TransCAD, this coverage can be related to other geographical phenomena; for example, road accidents weighted by traffic density, residential and commercial property values, or the impacts of traffic noise. We are conscious that our road network still contains some errors, but the model allows these to be rapidly identified.
 

 
Table 4 Quebec metropolitan region, Fall of 1991,
Travel time and route length by gender, transportation mode and journey type,
Typical weekday simulation summary statistics
Women
Men
Journey to (mode)
Travelling time (min.)
Route length (km)
Travelling time (min.)
Route length (km)
(a) Working place (car drivers) 
trips 64213  64213 93392  93392
Mean 12.10  8.94 13.00  9.84
St. dev. 23.82  23.01 24.57  24.25
(b) Working place (car passengers) 
trips 14194  14194 6001  6001
Mean 12.05  8.87 12.20  9.06
St. dev. 22.79  21.71 23.97  23.39
(c) Working place (taxi passengers) 
trips 225  225 324  324
Mean 6.18  3.47 11.34  8.45
St. dev. 11.22  8.67 26.51  27.13
(d) Shopping place (car drivers) 
trips 22502  22502 20757  20757
Mean 8.78  6.36 9.12  6.64
St. dev. 18.78  17.85 20.37  19.54
(e) Shopping place (car passengers) 
trips 14845  14845 2569  2569
Mean 9.49  7.04 10.04  7.53
St. dev. 20.93  20.83 19.75  19.35
(f) Shopping place (taxi passengers) 
trips 211  211 39  39
Mean 7.46  5.22 7.41  5.67
St. dev. 18.48  19.97 9.46  11.68
 

            Computed with SPSS using GLM General factorial and OD survey Expansion factorOverall, the computing speed of TransCAD to carry out route simulation was impressive and beyond expectations. However, even after personal communication with Caliper's staff, it was impossible to obtain details about the type of algorithms used in their package. The results look credible but we cannot verify their relevance using scientific criteria. The GISDK language is very powerful and efficient, but our programming task was jeopardised by many mistakes in the programmer's guides. We even had to guess the exact syntax and results format of some commands used in our application, due to poor and confusing documentation and examples. The procedure needs moderate hardware and software investment (< 15,000 US$). Personnel training is mandatory, but short, since all software packages (e.g. MapInfo and TransCAD) are user-friendly.
 
5. Conclusion
The preceding paragraphs illustrate clearly the usefulness of including both time and distance in studies of urban travel (Makin et al. 1997). Indeed, the traditional uses of OD surveys substantially under-use the richness and variety of data they contain. Preliminary results indicate that it is possible to combine GIS and transportation modelling to estimate travel time of urban commuters. This could help measuring temporal constraints of households planning their daily activities (Arentze et al. 1993; Miller 1991). It should also enhance OD surveys in order to improve analysis of urban dynamics.
        The strategy used to simulate commuters trips in the Quebec metropolitan area illustrates the benefits of extending the capacity of existing GIS providing efficient and task oriented simulation procedures using full integration (one software) or tight coupling strategies (interoperability). The demand for a comprehensive and behaviour-compatible route simulation system in transportation industry is tremendous. Applications include the comparison of various public transportation routes between two points, a better evaluation of demand for transportation resulting in closely adapted services, and the optimisation (yet to be defined) of public transportation journeys, to mention only a few. With such systems, the comparison of travel time between car and public transportation on a large scale will be possible by aggregating of individual trips characterised by the socio-economic attributes of commuters though to influence their likely behaviour (modal choice, elasticity of time cost, family style, etc.).
        The procedure presented here admittedly suffers from some limitations, among others the fact that the route actually selected may be only one among the likeliest, but not necessarily the shortest one (Gopal and Smith 1990). Ideally the modelled route should be the most probable, at least one of the more likely, considering travel time. Moreover, it is clear that people moving around do not always follow the shortest route (time-wise or distance-wise) but rather travel with due regard to other considerations (Hanson and Huff 1988) such as security, landscape and environmental quality, or stops related to family life (kindergarten, school, grocery store, etc.).
        Nevertheless, the shortest path hypothesis is probably among the best that can be used to exploit data coming from OD surveys, at least in their current state. Transportation simulation could also be improved upon by direct observation of vehicles equipped with GPS or the use of interviews and travel diaries (Lee-Gosselin 1996; Doherty and Miller 1997; Ben-Akiva and Bowman 1995). However, the overall costs would be so high that it seems reasonable to apply such methods to small, high-quality samples from which behavioural mechanisms can be better understood and the assumptions in behavioural models modified accordingly. Meanwhile, under present economic conditions and technologies, it appears more reasonable to rely primarily on route simulations to improve our understanding of population mobility and transportation planning at the scale of urban regions.
        Trip duration generated with this procedure will be used for other methodological or applied research. It will enable:

References
Adamson, P. and E. Tick  (1991) "Greedy Partitioned Algorithms for the Shortest-Path Problem." International Journal of Parallel Programming, 20(4): 271-298.

Arentze, T., A. Borgers and H. Timmermans (1993) "A Model of Multi-purpose Trip Behavior." Papers in Regional Science 72(3): 239-256.

Ben-Akiva, M. E. and J. L. Bowman (1995) "Activity-based Disaggregate Travel Demand Model System with Daily Activity Schedules." In Conference on Activity-Based Approaches: Activity Scheduling and the Analysis of Activity Patterns, Eindhoven, The Netherlands.

Blumen, O. and A. Kellerman  (1990) "Gender Differences in Commuting Distance, Residence, and Employment Location: Metropolitan Haifa 1972 and 1983." Professional Geographer, 42(1): 54-71.

Caliper Corporation (1996) TransCAD: Transportation GIS Software Reference Manual, Version 3.0, Newton, MA.

Camstra, R. (1996) Commuting and Gender in a Lifestyle Perspective. Urban Studies, 33(2), 283-300.

Claramunt, C. and M. Thériault  (1996) "Toward Semantics for Modelling Spatio-temporal Processes within GIS." In Advances in GIS Research II, M.J. Kraak and M. Molenaar Eds., London, Taylor & Francis, 27-43.

Claramunt, C., M. Thériault and C. Parent  (1998) "A Qualitative Representation of Evolving Spatial Entities in Two-dimensional Topological Spaces." In Innovations in GIS 5, S. Carver Ed., London, Taylor & Francis, 128-138.

Des Rosiers, F., A. Lagana, M. Thériault and M. Beaudoin  (1996) "Shopping Centers and House Values: An Empirical Investigation." Journal of Property Valuation and Investment. 14(4): 41-62.

Doherty, S. T. and E. J. Miller  (1997) "Tracing the Household Activity Scheduling Process using one-Week Computer-Based Survey." In Proceedings of the Eighth Meeting of the International Association of Travel Behaviour Research, Austin, TX.

England, K.V. L. (1993) "Suburban Pink Collar Ghettos: The Spatial Entrapment of Women." Annals of the Association of American Geographers, 83(2): 225-242.

Etches, A., C. Claramunt, A. Bargiela and I. Kosonen 1998. "An Integrated Temporal GIS for Model Traffic Systems." GIS Research UK VI National Conference, University of Edinburgh, UK.

Gärling, T. and E. Gärling (1988) "Distance Minimization in Downtown Pedestrian Shopping Behavior." Environment and Planning A 20: 547-554.

Golledge, R. G., M.-P. Kwan and T. Gärling (1994) "Computational Process Modeling of Household Travel Decisions using a Geographical Information System." Papers in Regional Science, 73(2): 99-117.

Gopal, S. and T. R. Smith  (1990) "Human Way-finding in an Urban Environment: A Performance Analysis of a Computational Process Model." Environment and Planning A 22: 169-191.

Gordon, P., H. W. Richardson and M.-J. Jun (1991) "The Commuting Paradox Evidence from the Top Twenty." Journal of the American Planning Association, 57(4): 416-420.

Hanson, S. and J. Huff (1988) "Systematic Variability in Repetitious Travel." Transportation 15: 111-135.

Hanson, S. (1995) The geography of Urban Transportation (Second Edition). New-York: The Guilford Press.

Johnston-Anumonwo, I., S. McLafferty  and V. Preston. (1995) Gender, Race and the Spatial Context of Women’s Employment. In Gender in Urban Research, edited by J. A. Garber and R. S. Turner, Urban Affairs Annual Review 42. Sage Publications, pp.  236-255.

Khoong, C. (1993) "Shortest-Path Reconstruction Algorithms." The Computer Journal, 36(6): 588-592.

Korem  (1998) MapLogix Version 2.0. Topological Map Editing Utility for MapInfo Professional. Http://www.korem.com/maplogix/index.html.

Lee-Gosselin, M. E. H. (1996) "Scope and Potential of Interactive Stated Response Data Collection Methods." In Household Travel Surveys: New Concepts and Research Needs, Conference Proceedings, Transportation Research Board, National Research Council, Washington, DC.

Makin, J., R. G. Healey and S. Dowers (1997) "Simulation Modelling with Object-Oriented GIS: A Prototype Application to the Time Geography of Shopping Behaviour." Geographical Systems 4(4): 397-430.

MapInfo Corporation  (1996)  MapInfo Professional Reference and User's Guide, Troy, NY.

Miller, H.  (1991) "Modelling Accessibility using Space-time Prism Concepts Within Geographical Information Systems." International Journal of Geographical Information Systems, 5: 287-301.

Pearn, W., L. Lea and L. Mao (1994) "Algorithms for the Windy Postman Problem." Computers & Operations Research, 21(6): 641-651

Preston, V. and S. McLafferty (1993) Gender Differences in Commuting at Suburban and Central Locations. Revue canadienne des sciences régionales, 16(2), 237-259.

Sedgewick, R. (1990) Algorithms in C. Addison-Wesley Publishing, United-States, 657 pages.

Thériault, M., P. Lemieux, R. Sirois and P. Villeneuve (1995) Géobase du réseau routier public de la région de Québec. Format Mapinfo 3.0, CRAD, Laval University, Québec.

Thomas, C., M. Beaudoin and M. Thériault  (1996) "Méthodologies de localisation et de classification socio-professionnelle: le cas de l'enquête O-D 1991 de la STCUQ." Cahiers de Géographie du Québec, 40(109): 69-90.

Villeneuve, P. and D. Rose (1988) "Gender and Separation of Employment from Home in Metropolitan Montreal, 1971-1981." Urban Geography, 9: 155-179. 

Acknowledgements  We gratefully acknowledge Paul Villeneuve, Martin Lee-Gosselin, Corinne Thomas, Pierre Lemieux, Frédéric Vachon, Raynald Sirois and Yanick Aubé for their valuable help at various stages of this research. This project was funded by the Quebec Province FCAR program, the Canadian SSHRC and the Canadian NSERC. It was realised in close co-operation with the STCUQ (Quebec Urban Region Transit Society) and the Quebec Province's Ministère des transports. 

ContentsJGIDA vol. 3, no. 1
Journal of Geographic Information and Decision AnalysisJGIDA Home