
Journal
of Geographic Information and Decision Analysis, vol.3, no.2, pp.1-8
The Classification of Quality
of Life Using Multi-criteria Analysis
Bryan H. Massam
Department of Geography and
Division of Social Science, York University, Toronto, Canada
bmassam@yorku.ca
Contents
1.
Introduction
2.The
generic QoL classification problem
3.
The
Aspiration Interaction–level Model (AIM)
4.
Analysis of hypothetical data
5.
Conclusions
References |
ABSTRACT
After a brief review
of selected literature on quality of life (QoL) the paper considers the
use of multi-criteria analysis for classifying individuals using data for
a set of independent factors. A generic QoL classification problem is defined.
A review and critique of a standard multi-criteria procedure which uses
a simple additive weighting (SAW) model is provided. The problem of determining
weights for factors for use in a SAW model is identified. Using hypothetical
data for 11 individuals and 9 factors relating to quality of life a multi-criteria
method which does not require the user to stipulate explicit weights for
the factors is used to provide a classification of the individuals. The
classification ranks the individuals in terms of their QoL from best to
worst. Reference individuals are included in the data set to interpret
the results. The method is the Aspiration-level Interaction Method (AIM).
The merits of AIM for assisting policy makers determine allocations of
resources among factors to improve QoL are presented. Alternate scenarios
for allocating resources among factors are evaluated.
KEYWORDS:quality
of life, multi-criteria analysis, simple additive weighting model, aspiration
interaction-level model, resource allocation, policy making. |
1.
Introduction
Public policy-making in the fields of social services often focuses
on the protection and improvement of the quality of life (QoL) for individuals
and communities. Recent studies on QoL include surveys undertaken by the
United Nations Development Programme at the aggregate level of the state
to provide a ranking of states in terms of a Human Development Index (HDI).
Details regarding the HDI are available on the website (www.undp.org/hdro).
This index is calculated using empirical scores on three basic indicators
relating to education, health and income. A simple additive weighting (SAW)
model is used to calculate dimensionless scores using standardized values
of the raw data. A number of other studies using objective and subjective
indicators for a variety of observation units such as census tracts, cities
and regions have been reviewed by Murdie et al.
(1992).
Typically many of these studies use approaches based on economic, social,
political and environmental indicators, and they rely on SAW models to
produce maps of well-being, livability, sustainability and QoL. Smith’s
(1974) work on social indicators to identify areas of deprivation in cities,
for example, is well known as part of his welfare approach to human geography.
GIS are now used to produce maps of well-being and QoL. The causative linkages
between objective and/or subjective scores, levels of performance or satisfaction
levels on indicators and well-being, social needs and outcome levels for
individuals in terms of health, education, economic prosperity, happiness,
the capacity to cope and take control of life chances and opportunities,
have been explored by a number of researchers.
A variety of empirical studies
on QoL in urban areas around the world is presented in Yuan
et al (1999). A large-scale study on QoL of citizens in Ontario has
been undertaken by a team at the Quality of Life Research Unit at the University
of Toronto. Details are available on the web site (www.utoronto.ca/qol).
Another web site (www.torontovitalsigns.com) provides useful information
on a current study in Toronto on the QoL in the city and a number of linked
websites offer complementary information on a wide range of QoL studies.
The QoL study at the Quality
of Life Research Unit (Brown et al 1998) uses
a detailed questionnaire distributed to selected individuals who provide
responses to a 5-point scale concerning the importance of specific indicators
and the level of satisfaction for each indicator. A value greater than
3 for an indicator suggested a positive contribution to QoL, whereas a
score of less than 3 contributes negatively. A score of exactly 3 is neutral.
Contextual information is provided by asking each respondent to comment
on their opportunities and control over life-styles. The indicators are
defined and organized in such a way as to reflect three fundamental dimensions
of QoL of an individual namely, ‘being’, ‘belonging’ and becoming’. These
three dimensions are each divided into three characteristics and each of
these is described by a number of indicators. Elaboration of these important
terms on the "nine areas of the life" is included in the questionnaire
(Brown et al 1998, p. 1).
In this paper I will outline
a generic quality of life classification problem in a way that allows it
to be tackled using multi-criteria analysis. One specific type of analysis
will be used to classify a set of observations using a hypothetical data
set which comprises eleven individuals and nine indicators. Whereas many
multi-criteria classification techniques require explicit data on the relative
importance of the indicators expressed as a set of weights, or a pair-wise
comparison, the technique used in this paper does not require this information.
The technique to be used is the Aspiration Interaction-level Model (AIM)
as developed by Lotfi et al (1998).
Following this introduction
the next section of the paper will offer brief comments on the general
problem of classifying QoL of individuals using multi-criteria analysis.
This will be followed by a description of AIM. The results of the analysis
will be offered with general conclusions regarding the merits of multi-criteria
analysis for tackling the generic problem and assisting in the evaluation
of public policy-making which focuses on improving quality of life.
2.
The generic QoL classification problem
The problem can be stated thus:
Given a set of observation units, for example, states, regions, cities,
census tracts or individuals (I1….IN), and a set
of factors, indicators or criteria which characterize independent components
of QoL (F1 . . . Fk), and for each an achievement
score (Sij – score for individual i for Factor j) combine the scores for
all factors into a single QoL score for each individual.
Among the information required to tackle this problem has to be included:
the importance of the factors, for example, are they all equally significant
in contributing to QoL?
the type of data used to describe the scores: ranks, ratio data, non-commensurate
values etc.
the procedure for combining scores-additive, multiplicative, cumulative
etc.
Overall it is important that
the procedure used for tackling the problem be transparent, so that the
analysis can be replicated and it is traceable. Further, it is necessary
that the arguments and logic of the procedure be credible in order that
legitimacy be enhanced and so that those who use the results have faith
in the exercise. Finally, in order to assist public policy-making it is
useful to provide information on QoL in such a way that alternate policies
can be evaluated and compared, and a preferred policy defended. With this
in mind, if we have alternative rankings of individuals using different
policy scenarios regarding the weighting of the factors then it is possible
to determine which individuals benefit or suffer under each policy. This
approach typically uses aggregate analysis as the same set of weights is
assigned to the factors by each individual.
The SAW model is often used
to tackle the generic QoL classification problem. The justification relies
on a number of assumptions, for example, that the raw objective data or
the subjective data can be made or are commensurate, so that a compensatory
model can be applied. Recently Malczewski (2000)
has review assumptions regarding linear models as used in GIS.
Hwang
and Yoon (1981, p. 99) suggest that the "simple additive weighting
(SAW) method is probably the best known and very widely used method of
Multi-Attribute Decision Making". While we might contest the legitimacy
of using a simple additive function for combining scores in order to obtain
a single value for each individual it has been argued by Hwang
and Yoon (981, p. 103) that "theory, simulation computations, and experience
all suggest that the SAW method yields extremely close approximations to
very much more complicated non-linear forms, while remaining far easier
to use and understand".
An interesting review of
the errors which can be associated with the use of SAW models is given
by Rowe and Pierce (1982). They use hypothetical
data and introduce errors of known types and magnitudes in an attempt to
determine "in a general way the sensitivity of the weighting summation
decision model to some of the classes of error to which it is subject."
For those who rely on the use of SAW to tackle the classification problem
it is most important that clear recognition of the potential errors be
incorporated into the study, and specifically that sensitivity tests be
run as part of the analysis. Solomon and Haynes
(1984) also conclude that while there are a variety of models for accumulating
impacts into a final score, "the use of the simple weighting summation
model is probably justified." It is the use of a formal single dimensionless
number which causes considerable problems for anyone who wished to use
the results and participate in a debate which involves compromises, trade-offs
and a discussion of scores and trade-offs among factors. The aggregation
of impacts across a wide range of variables is worrying to policy makers.
Some argue that the score for a particular individual is not a simple additive
function of the worth of the various components or even a readily identifiable
multiplicative function, for that matter. This is stressed in a paper by
Roy
and Bouyssou (1986). In philosophical terms we are reminded of the
debate propounded by Moore in Principia Ethica when he argued that
"the worth of what he termed an organic whole bears no regular proportion
to the sum of the values of its parts". In particular, "the value of a
whole must not be assumed to be the same as the sum of its values of its
parts" (Rosenbaum, 1975, p. 127). Yet this concern
does not seem to hinder the development of the additive models. However,
we can observe that there appears to be limited dialogue between theoreticians
and practitioners in this area. One or two notable examples of cooperation
should be mentioned, for example, the work of Keeney
(1972) and the examples provided by Edwards
(1971).
We should further note that
if we wish to defend the use of a simple additive model the following two
conditions should be satisfied. First, the preferences for, or the trade-off
for pairs of factors, for example Fr and Fs should
be preferentially independent of fixed levels for any other factors, for
example Ft. Second, that Fr, for example, should
be utility independent of the other factors. Intuitively these conditions
are appealing however very rarely are they verified prior to the application
of an additive model. One case of verification is given by Keeney
and Nair (1977) in their study on the use of a set of six criteria
for evaluating nine alternate sites for a nuclear power plant in the Pacific
northwest of the U.S.A. They use the Multi Attribute Utility Theory approach.
The verification of the two conditions depends upon the confidence we can
attach to opinions regarding the trade-offs among factors at hypothetical
levels. These types of questions are obviously not easy to pose in manageable
practical ways to the various interest groups.
The SAW model requires a
set of weights for the factors, and one of the challenges facing the analyst
is to justify a particular set. There is no single agreed methodology for
determining the so-called correct weights. Alternate strategies for determining
weights are reviewed in Massam (1993). Intuitively
and experientially it is clear that not all factors are of equal importance
in their contribution to QoL, yet the problem remains as to how best to
determine an appropriate set of weights that accurately reflect preferences
and opinions. In the next section the multi-criteria technique AIM is described
and this technique does not require explicit weights for each factor to
be defined at the outset.
3.
The Aspiration Interaction–level Model (AIM)
Basically this model requires three pieces of information for each
factor: an ideal value (Ii), a nadir value (Ni) and
a desired/acceptable or aspiration value (Ai). Scores for each
factor for each individual are required. It can be argued that Ii
and Ni represent maximum and minimum scores (best or worst scores)
for each factor, while Ai can be set to reflect a subjective
level or achievement which is aspired to. For example, if Ai =
Ii this implies that a lot of importance is attached to the
factor i and a high weight should be assigned. However, if Ai =
Ni then the reverse is the case. "The idea of the approach [AIM]
is based on . . . the concept of a ‘satisficing solution’ rather than .
. . the traditional ‘optimal solution’. Levels of aspiration are used to
explore the set of non-dominated solutions, see Giocoechea
et al. (1982) by having the decision maker establish levels of aspiration
and then obtain some feedback about the reasonableness of these levels
and the alternatives satisfying them . . . The nearest solution [to the
aspiration solution] is defined as the alternative that minimizes a scalarizing
function proposed by Wierzbicki (1979); with a weight on criterion i
given by (Ai-Ni)/(Ii-Ni), where
Ai is the aspiration level, Ni is the nadir value,
and Ii is the ideal value for criterion i. "The nearest
solution is then an alternative that minimizes the expression
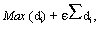
with
di = (Ai-Ni) (Ai-xik)/(Ii-Ni)2
and , 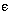 positive but small, where xik is the value of alternative
k in terms of criterion i. See Lotfi et al (1988)
for more details." (Lotfi 1989, p.14).
positive but small, where xik is the value of alternative
k in terms of criterion i. See Lotfi et al (1988)
for more details." (Lotfi 1989, p.14).
Alternate values for Ai
can be used to describe different policy scenarios. For example, if it
is assumed that all the factors are equally important then Ai
can be set to Ii for each factor, however if it is felt that
those factors concerning ‘being’ are of no importance then for these factors
Ai can be set to levels at Ni, or close to this.
Under different scenarios perhaps different ranking of the individuals
may result and this information can be used to assess alternative policies.
For instance if certain individuals rank high when a particular set of
factors is weighed heavily then a policy that focuses on improving these
factors will yield benefits to these individuals.
Table 1 Hypothetical
data set
Being
Belonging
Becoming
|
|
F1
|
F2
|
F3
|
F4
|
F5
|
F6
|
F7
|
F8
|
F9
|
|
I1
|
4
|
5
|
4
|
2
|
1
|
2
|
2
|
3
|
2
|
|
I2
|
3
|
2
|
2
|
4
|
5
|
4
|
4
|
3
|
4
|
|
I3
|
1
|
1
|
1
|
5
|
5
|
5
|
3
|
3
|
3
|
|
I4
|
5
|
5
|
5
|
1
|
1
|
1
|
3
|
3
|
3
|
|
I5
|
5
|
5
|
5
|
3
|
3
|
3
|
1
|
1
|
1
|
|
I6
|
4
|
3
|
4
|
4
|
3
|
4
|
4
|
3
|
4
|
|
I7
|
3
|
4
|
3
|
3
|
4
|
3
|
3
|
4
|
3
|
|
I8
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
I9
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
|
I10
|
1
|
2
|
3
|
3
|
4
|
5
|
1
|
5
|
5
|
|
I11
|
3
|
3
|
3
|
3
|
3
|
3
|
3
|
3
|
3
|
Note(1): A score of 5 on a factor is the highest
value and contributes positively to QoL. A score of 3 represents a neutral
contribution to QoL. A score less than 3 represents negative contributions
to QoL.
I9: has the overall highest QoL with 5 for
each factor. I8: has the overall lowest QoL with 1 for
each factor. I11: is a marker individual separating, positive
from negative scores for QoL
4.
Analysis of hypothetical data
A hypothetical set of data is given in Table
1. There are eleven individuals and the nine factors are grouped into
three sets to represent ‘being’, ‘belonging’ and ‘becoming’, following
the concepts presented by Brown et al (1998)
mentioned earlier. Using the data in Table
1 four experiments were conducted under different assumptions regarding
the aspiration levels for the factors. Each experiment generated a different
ranking of the individuals from the highest to the lowest QoL. Details
of the experiments are given on Figure 1 with the results.
If all factors are equally important then only three individuals rate better
than the marker I11. However, if emphasis is placed on specific
groups of factors, while setting the aspiration level to 3 for all the
other factors, then many more individuals appear to have an overall positive
quality of life, that is a score superior to the marker I11.
If emphasis is placed upon the three factors concerning ‘being’ (F1,
F2, F3) then individuals I2, I10,
I3 and I8 have negative QoL scores. For experiment
3, which places emphasis on the factors concerning ‘belonging’ (F4,
F5, F6), individuals I1, I4
and I8 have negative QoL scores. Finally, for experiment 4 which,
places emphasis on F7, F8 and F9, the
factors relating to ‘becoming’, individuals I1, I10,
I5 and I8 have negative QoL scores. On Figure
1 lines to join individuals for each experiment indicate the shifts
which occur. While I9 and I8 occupy the stable end
positions as best and worst QoL respectively the variations in markings
are interesting. For example, only individuals I6 and I7
have positive QoL scores for all experiments. I10 is consistently
low, only for experiment 3 is a modestly positive QoL score recorded. I2
moves from negative values for experiments 1 and 2 to very positive scores
for experiments 3 and 4.
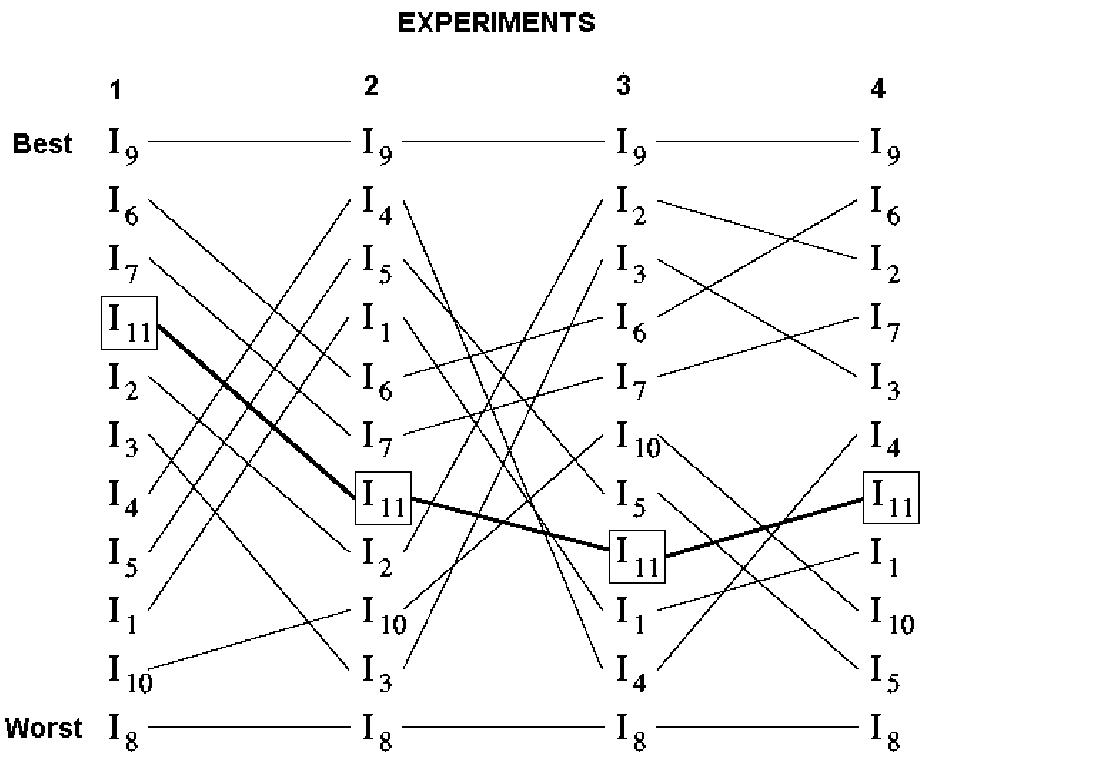
Figure 1. Classification of individuals: four experiments;
Experiment 1: all factors equal (Ai =
Ii );
Experiment 2: F1, F2, F
3 set to ideal value (5) other factors set to 3;
Experiment 3: F4, F5,
F6 set to ideal value (5) other factors set to 3;
Experiment 4: F7, F8, F9
set to ideal value (5) other factors set to 3.
5. Conclusions
The significance of the shifts in ranking provides useful information
for policy makers. For example, if a finite set of resources is available
to allocate among the factors to improve QoL then the question is what
proportion should be allocated to each factor to achieve the greatest improvement
in QoL? If we assume the total resource to be allocated is unity
1.0, then the allocation to the factors can be represented by the weights
assigned using the AIM algorithm. For experiment 1, the weights for each
factor are (0.111). The sum is unity. However, for experiment 2, 3 and
4 the weights assigned to the most important set of three factors is (0.167x3),
while the other factors receive (0.083x6). the allocation of weights that
generates the least number of individuals with positive QoL scores is the
"all equal" experiment that allocates resources equally among all the factors.
If resources are allocated to one of the three clusters that focuses on
‘being’, ‘belonging’ or ‘becoming’ then many more individuals enjoy positive
QoL scores. Experiment 3 is perhaps the preferred one in terms of generating
the largest number of positive QoL scores, though individuals I1,
I4, and I8 remain with low scores and probably deserve
special individual attention.
In summary I suggest that
AIM is a useful multi-criteria technique to classify individuals in terms
of scores for independent factors relating to QoL. A particularly interesting
feature of AIM which makes it useful concerns the ability of the user to
assign aspiration levels for each factor, and hence avoid the difficulties
of defining explicit weights or measures of importance for the factors,
which is a key part of the SAW method. By conducting a series of experiments
with AIM using different aspiration levels to represent alternate policies
then the effects on the ranking of individuals using QoL scores can be
examined. From a public policy-making perspective it is important to link
the descriptive aspects of multi-criteria analysis to prescriptive approaches
which help to use public resources more effectively. I suggest that a multi-criteria
technique like AIM has a useful role to playing in this regard.
.References
Brown, I. Raphael, D. and Renwick, R. 1998 Quality of Life Profile,
Adults (full version), Quality of Life Resources, Adult Series. Item
#2-1, Quality of Life Research Unit, Centre for Health Promotion, University
of Toronto, Toronto.
Edwards,W. 1971 "Social Utilities", Engineering Economics,
Summer Symposium, Series 6.
Giocoechea, A. Hansen, D.R. and Duckstein, L. 1982, Multi-objective
Decision Analysis with Engineering and Business Applications, New York:
Wiley.
Hwang, C.L and Yoon, K. 1981 Multi-Attribute Decision Making,
New York: Spring Verlag.
Keeney, R.L. 1972 "Utility functions for multi-attributed consequences",
Management
Science, 19, 276-287.
Keeney, R.L. and Nair, K. 1977. Selecting nuclear power plants
in the Pacific Northwest using decision analysis, in Bell, D.E. Keeney,
R.L. and Raiffa, H., Conflicting Objectives in Decisions, New York:
Wiley.
Lotfi, V. 1989 "An aspiration-level interactive method (AIM)
for decision making," Operations Research Letters, 8, 113-115.
Lotfi, V., Stewart, T.L. and Zionts, S. 1988 "An aspiration-level
interactive method for decision making", Working Paper #701, School of
Management, State University of New York at Buffalo, Buffalo, New York.
Malczewski, J. 2000 "On the use of weighted linear contribution
method in GIS: common and best practice approaches" Transactions in
GIS, 4(1), pp. 5-22.
Massam, B.H. 1993 The Right Place: shared responsibility and
the location of public facilities, London: Longman.
Murdie, R.A Rhyne, D. and Bates, J. 1992 Modelling Quality of
Life Indicators in Canada: a feasibility analysis, York University, Institute
for Social Research.
Rosenbaum, S.P. (Ed) 1975. The Bloomsbury Group, Toronto: University
of Toronto Press.
Rowe, M.D. and Pierce, B.L. 1982 "Some tests of analytical multi-objective
decision-making methods", Socio-Economic Planning Sciences, 16,3,
133-140.
Smith, D.M. 1974 "Who get What Where and How: a welfare focus
for human geography," Geography 59, pp. 289-297.
Wierzbicki, A.P. 1979 "The use of reference objectives in multi-objective
optimization, working paper #79-66. International Institute for Applied
Systems Analysis, Laxenburg. Austria.
Yuan, L.L. Yuen, B. and Low, C. (eds) 1999 Urban Quality of Life:
critical issues and options, Singapore: School of Building and Real Estates.
AcknowledgementsThis
project was supported by a research grant from the Faculty of Arts, York
University, Toronto, Canada.
 JGIDA vol. 3, no. 2
JGIDA vol. 3, no. 2
 JGIDA Home
JGIDA Home
