Basic Measurement and Basic Operations II

Reading Corner

• Chapter 2: Should be read by now

Reading Assignment for next week:

• Chapter 3: “Maps as Numbers”
• (Note: slightly ahead of the outline, to take pressure off of slack week...)

The Structure of Today’s Lecture:

• Basic Measurement
• Announcements
• Basic Operations II

Basic Measurement

• Basic distance measurement —
  • Measuring single straight distances.

An operation for measuring a set of distances

• Spread

What it does:

• Measures distances from designated cells

Spread and its modifiers

• Euclidean version (simple spreading)

Syntax:

• DistanceSurface = Spread map to maximum distance;

Explanation of the operation and its modifiers

• This operation generates a map of spatial distances from target (non-VOID) cells in the operand map to the maximum distance or cost specified by the to modifier.

The units and the precision are specified in maximum distance

• (eg. 30km, 30.km, 30.00km are all different)

Spread is commonly known as a buffering operation

• Buffers from linear features are sometimes termed corridors.

Distance is arguably the most basic among spatial relations

• Spread explicitly measures space. It is a fundamentally spatial function.
• Almost all examples of what a GIS does use a buffers example—ad nauseum.

An Example (from Simple Computer Imaging and Mapping):

• Measuring distances from a road.

Other Examples

Using Spread to isolate the perimeter of lakes:

• Do we want the water or the beach?

There are several ways to view the results of Spread

A spreading nucleus ‘centered’ view

• Distances increase from the nuclear spreading cells outward.
• How far is X from the nucleus?

A question regarding a multi-cell ‘clot’:

• Rob's Question:
  • What happens when the spreading cell is encased by other spreading cells?
  • Spread always measures distances from the nearest cell.

A view from the ‘periphery’ at a target cell

• The distance from a non-nuclear point on the measured plane toward a target.
• The view from the other cells.

In which of the 2 ways does the algorithm work?

A third view: “as the helicopter flies”

• the overall pattern.

A fourth view: the underlying structure — the Distance Surface

• The DistanceScape and its pits, basin slopes and ridge lines
• Question: When do we get hill/mountain slopes and peaks?
• Using image processing it is possible to show the DistanceScape as a shaded (distance) relief image. (Figure)

Ridge lines delineate Thiessen Polygons

Are Thiesen Polygons (aka Voronoi Diagrams ) doable in raster as well as in vector,

• and does that capability exist in MFworks?

Note that buffers are often portrayed by applying a Recode of every n^th distance to the result of Spread

• This in effect results in contour-like distance isolines.

Spread is described as a wave of distance measurements that propagate outward from a spreading cell

• what happens to the distances between spreading cells when there are many spreading cells, bearng in mind that the computation is NOT parallel?

Spreading takes time

• There are a lot of distances to be measured.
• The spread algorithm calls for backtracking.
• Iterations compound the amount of computation.

Even so, the euclidean spread is relatively fast compared to its cousin—the non-linear Travel Cost (“Friction”) Spread

• At this point we are only introducing the Euclidean version of Spread.
  • This spread operation is performed by a fast algorithm module.
  • The simple spread is performed far more frequently than its fancy relative.

Non-linear distances, topographic distances, and network spreading will be described under the Rarely Used Operations category.

• They are implemented by the travel-cost spread module.

Announcements

• Assignment 3 is here
• Work on it asap, e.g. starting next week
• by ‘killing’ Assignment 2 quickly, or
• in parallel with Assignment 2

The first Ombusperson Meeting will be held next week

• Craig Savill cesavill@julian.uwo.ca
• Tracee Nemeth tnemeth@julian.uwo.ca

GIS 2000

• Questions on this?
• One day early student registration is $ 50.-
• State your day: Tuesday, Wednesday or Thursday
• “Calling all Registration Forms”
• for those wishing to attend
• There will be a lecture that week

Basic Operations II

• Arithmetic
• Basic Logic
• Set Overlay (logical map overlay)
  • AND, OR, NOT
  • Cross
  • Combine
• More on Layer Superimposition

Basic Operations II

• Basic Operations on n layers

Overlay Arithmetic

What these Operators and Functions do:

• Arithmetic expressions are commonly applied to cells on 1 or more layers.

Between cells stacked on different layers.

• For example, calculating the Standard Deviation of 40 annual Rainfall layers.

Between 1 layer and a constant.

• Example: determining whether/where a maxima condition is met.

Note that the implementation is not as individual operations.

Rather, in MF works

• these functions are implemented under the Operators and Function menus of the Script window.
• Question: What’s the reason for this ‘preferential’ treatment?

The Answer:

• Mainly because of the mathematical nature of these functions.
• It is possible to use these functions in an Algebraic Statement.

There are common conventions for building

• Algebraic Statements.

The MFworks documentation describes the:

• Syntax
• Operators
• Functions
• Order of operations
• Mixed mode arithmetic
• VOID data

On-line documentation may help use these core ‘map algebra’ features

Basic Logic

*** Logic and its implementation in MFworks may well be on the test(s) ***

The vocabulary of logic

• the Propositional Calculus
  • object term A , B
  • Binary World: True or False
  • Connectives

In our case object “A” really means:

• the Value Z of Cell [X,Y] on Map Layer A
  • and since many or all the cells are examined, we are really referring to a two-tiered (hierarchical) compound array variable object

Connectives — the base set

AND	^	(conjunction)
OR	v	(disjunction)
NOT	~	(negation)

additional connectives

• IMP —>
• A—> B 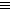~ (A ^ ~B) 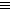~A v B
• EQUIV
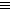
• (A —>B) ^ (B—>A) 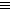(A ^ B) v (~A ^ ~ B)

other connectives

• XOR
• NAND

The Truth Table for

• A^B
• AvB
• A—>B
• AB

Let’s solve together:

To be continued next week...