CS 2120: Topic 10

Videos for this week:

Algorithms

What is an algorithm?

Algorithm = a set of instructions for performing a specific task; a “recipe” for solving problems

Python allows you to use any number of algorithms (i.e. list.sort()) without having to know about any of their implementation details

• this is a good thing when we want to just get things done

But, it’s also important to have a basic understanding of them

• this can help you to become a better programmer, abstract thinker, and problem solver — see computational thinking

We will cover three algorithms today: binary search, bubble sort, and merge sort.. one for each of the following categories:

• Searching
• Sorting
• Recursion

---

Warning

In this module we are moving away from using code and towards understanding how it works. As such, don’t expect to look at these algorithms and immediately understand how they work. They require careful study to make sense of. The best tool you have for understanding how they work is to carefully trace their operation, step by step. Trying to understand complex algorithms “all in one go” is a recipe for frustration. Take your time, and step through the algorithm (with pen and paper) on a small input to get a feel for what it’s doing.

Binary search

Let’s take a look at binary search:

def binary_search(list,val,left,right):
  while left <= right:

    midpoint = (left+right)/2

    if list[midpoint] > val:
      right = midpoint - 1
    elif list[midpoint] < val:
      left =  midpoint + 1
    else:
      return midpoint

  return -1

• On average, how many iterations through the loop does this function make?

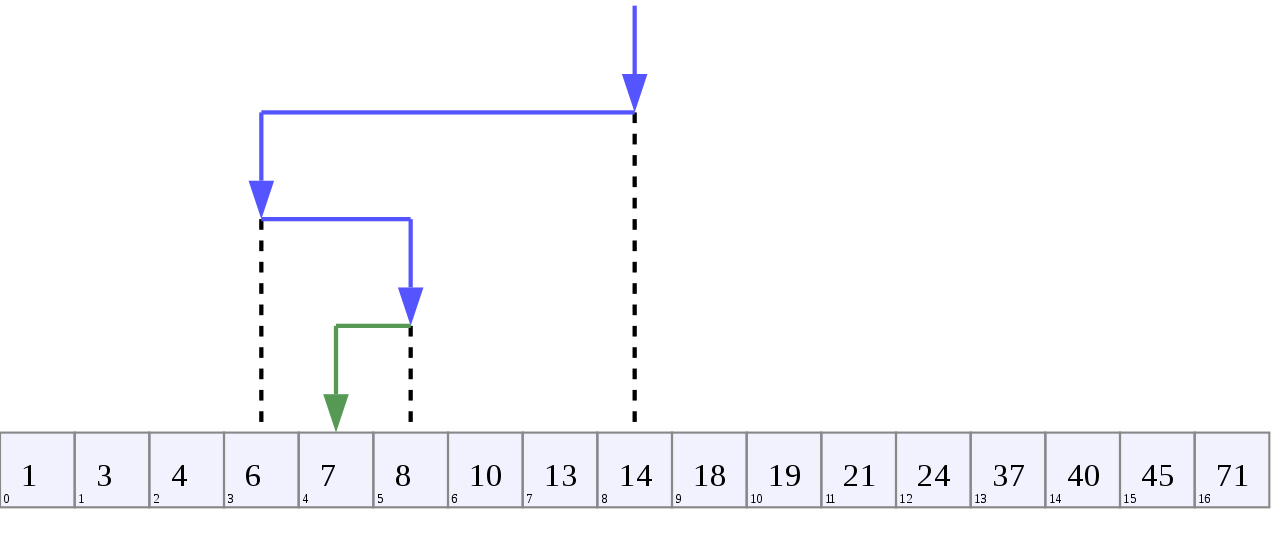
How it works

• You give me a sorted list (list), a value to search for (val), the left index (left) and right index (right)

• I cut the list in half by taking the midpoint

• If val is left of midpoint, val must be on the left half of the list, so re-assign right to equal midpoint - 1

• If val is right of midpoint, val must be on the right half of the list, so re-assign left to equal midpoint + 1

• If val is at the midpoint, we’re done

• Keep splitting the list and changing left, right, and midpoint until we find our value

• It’s called “binary search” because we are splitting the list into 2 pieces for each iteration.

Bubble Sort

Let’s take a look at bubble sort:

def bubble_sort(list):
   swap = True
   while swap:
      swap = False

      for i in range(len(list)-1):
         if list[i] > list[i+1]:
            tmp = list[i]
            list[i]=list[i+1]
            list[i+1]=tmp
            swap = True
   return list

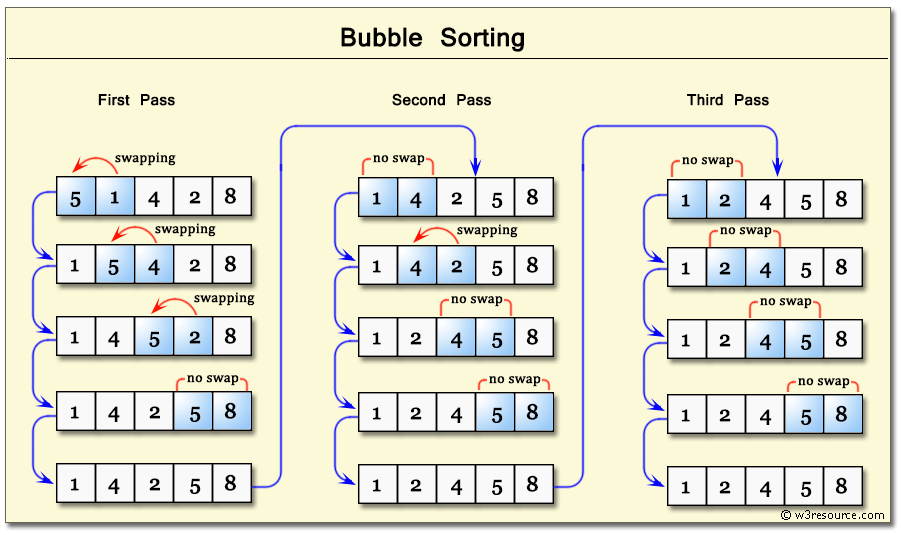
How it works

• You give me a list called list

• I scan through the list, looking at adjacent pairs of values.

• If I see a pair that is “out of order” (e.g., [17, 9] ), I swap the two values to be in order ( [9,17] ).

• I keep doing that until the list is sorted.

• It’s called “bubble sort” because the smaller values seem to “bubble up to the top”.

Is bubble sort the best?

• Definitely not… there are many better sorting algorithms

• With recursion, we can do Mergesort (better than bubble sort)

Recursion

• If a function calls itself, it is said to be a recursive function.

Writing a simple recursive function

• Every recursive function needs two things:

• A base case that terminates the recursion.

• A recursive step that calls the function again, but with a modified (probably smaller) parameter

Activity

Write a function fact(n) which computes the factorial of n using recursion (no loops allowed!).

Identify the base case and recursive step.

Mergesort

Remember this

There are many algorithms to solve any given problem.

• First, we need to implement a merge operation in Python:

  def merge(left, right):
     merged = []
     l=0
     r=0
     while l < len(left) and r < len(right):
        if left[l] <= right[r]:
           merged.append(left[l])
           l = l + 1
        else:
           merged.append(right[r])
           r = r + 1
  
     if l < len(left):
        merged.extend(left[l:])
     else:
        merged.extend(right[r:])
     return merged
  

• With merge defined, let’s take a look at merge sort:

  def mergesort(list):
     if len(list) <= 1:
        return list
     else:
        midpoint = int( len(list) / 2 )
        left = mergesort(list[:midpoint])
        right = mergesort(list[midpoint:])
        return merge(left,right)
  

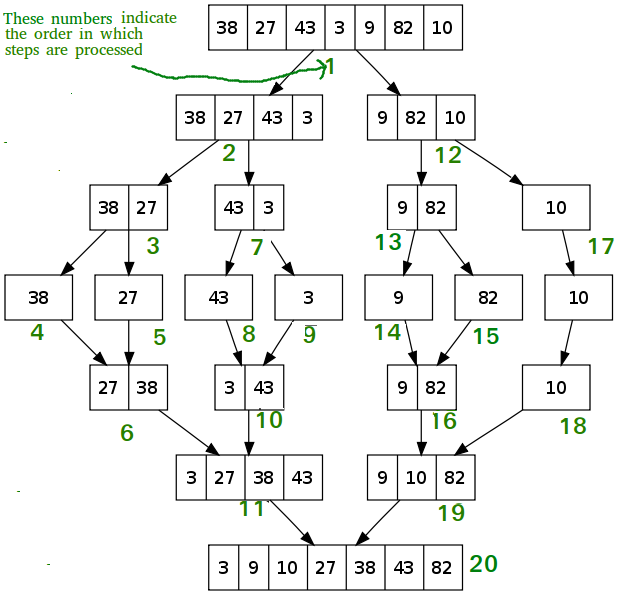
How it works

• You give me a list (list) with n elements

• I divide list into n sublists, each having 1 element.

• The sublists are now already sorted! (Any list with only one element is automatically sorted)

• I now begin merging sublists, to produce bigger (but still sorted) sublists:

• I compare the first element in one sublist to the first in the other

• Whichever is smaller goes into the merged list

• I now compare the second element in that list to the first element in the other list

• … and so on…

• I keep going until there is nothing left to merge (there’s only one big, sorted, list)

For next class

• If you’ve made it this far, congrats! Check out http://www.sorting-algorithms.com/ and see how bubble sort and merge sort compare to other popular sorting algorithms

• Work on Assignment 3 and Assignment 4